【题目】如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( ) 
A.4
B.8
C.16
D.无法计算
参考答案:
【答案】C
【解析】解:∵四边形ABCD是正方形, ∴∠ABC=∠D=90°,AB=AD,
即∠ABF=∠D=90°,
在Rt△ABF和Rt△ADE中,![]() ,
,
∴Rt△ABF≌Rt△ADE(HL),
∴SRt△ABF=SRt△ADE ,
∴SRt△ABF+S四边形ABCE=SRt△ADE+S四边形ABCE ,
∴S四边形AFCE=S正方形ABCD=16.
故选C.
【考点精析】本题主要考查了正方形的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
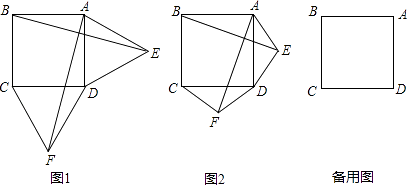
(1)请判断:AF与BE的数量关系是 , 位置关系是;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予说明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一人患了流感,经过两轮传染后共有100人患了流感,每轮传染中平均一个人传染的人数x满足的方程为( )
A.1+x+x(1+x)=100
B.x(1+x)=100
C.1+x+x2=100
D.x2=100 -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣2x=0的一次项系数是( )
A.2
B.﹣2
C.1
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的外角和是它内角和的
 ,求:
,求:
(1)这个多边形的边数;
(2)这个多边形共有多少条对角线. -
科目: 来源: 题型:
查看答案和解析>>【题目】轴对称图形只有一条对称轴_______(判断对错)
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x=2时,代数式ax3+bx+1的值为6,那么当x=﹣2时,这个代数式的值是( )
A.1
B.﹣4
C.6
D.﹣5
相关试题

