【题目】已知函数f(x)= ![]() x2+ax2+bx﹣
x2+ax2+bx﹣ ![]() (a>0,b∈R),f(x)在x=x1和x=x2处取得极值,且|x1﹣x2|=
(a>0,b∈R),f(x)在x=x1和x=x2处取得极值,且|x1﹣x2|= ![]() ,曲线y=f(x)在(1,f(1))处的切线与直线x+y=0垂直. (Ⅰ)求f(x)的解析式;
,曲线y=f(x)在(1,f(1))处的切线与直线x+y=0垂直. (Ⅰ)求f(x)的解析式;
(Ⅱ)证明关于x的方程(k2+1)ex﹣1﹣kf′(x)=0至多只有两个实数根(其中f′(x)是f(x)的导函数,e是自然对数的底数)
参考答案:
【答案】解:(Ⅰ)求导f′(x)=x2+2ax+b,由f(x)在x=x1和x=x2处取得极值, 则x1 , x2是方程x2+2ax+b=0的两个根,则x1+x2=﹣2a,x1x2=b,
由|x1﹣x2|= ![]() ,则(x1+x2)2﹣4x1x2=5,则4a2﹣4b=5,①
,则(x1+x2)2﹣4x1x2=5,则4a2﹣4b=5,①
由曲线y=f(x)在(1,f(1))处的切线与直线x+y=0垂直,
则f′(1)=1,
即2a+b+1=0,②,
解得: 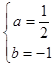 .
.
∴f(x)= ![]() x3+
x3+ ![]() x2﹣x﹣
x2﹣x﹣ ![]() ,
,
(Ⅱ)对于(k2+1)ex﹣1﹣kf′(x)=0,
当k=0时,ex﹣1=0,方程为实根,
当k≠0时,k+ ![]() =
= ![]() ,令g(x)=
,令g(x)= ![]() ,
,
g′(x)=﹣e ![]() =﹣e
=﹣e ![]() ,
,
当x∈(﹣∞,﹣1)∪(2,+∞)时,g′(x)<0,
∴g(x)的单调递减区间(﹣∞,﹣1),(2,+∞)单调递增区间(﹣1,2),
函数g(x)在x=﹣1和x=2处分别求得极小值和极大值,
g(x)极小=g(﹣1)=﹣e2<0,g(x)极大=g(2)= ![]() >0,
>0,
∴对于g(x)= ![]() ,由ex﹣1>0恒成立,
,由ex﹣1>0恒成立,
且y=x2+x﹣1时与x轴有两个交点,
从而g(x)无极大值,g(x)min=g(x)极小=g(﹣1)=﹣e2 ,
当k<0时,k+ ![]() ≤﹣2直线y=k+
≤﹣2直线y=k+ ![]() ,与曲线y=g(x)至多有两个交点,
,与曲线y=g(x)至多有两个交点,
当k>0时,k+ ![]() ≥2>
≥2> ![]() =g(x)极大 , 直线y=k+
=g(x)极大 , 直线y=k+ ![]() ,与曲线y=g(x)只有一个交点,
,与曲线y=g(x)只有一个交点,
∴方程(k2+1)ex﹣1﹣kf′(x)=0至多只有两个实数根.
【解析】(Ⅰ)由题意可知x1 , x2是方程x2+2ax+b=0的两个根,利用韦达定理及|x1﹣x2|= ![]() ,求得4a2﹣4b=5,由f′(1)=1,2a+b+1=0联立即可求得a和b的值,求得f(x)的解析式;(Ⅱ)由题意可知当k≠0时,k+
,求得4a2﹣4b=5,由f′(1)=1,2a+b+1=0联立即可求得a和b的值,求得f(x)的解析式;(Ⅱ)由题意可知当k≠0时,k+ ![]() =
= ![]() ,构造辅助函数,求导根据函数的单调性求得函数的极值及最值,利用基本不等式的性质,当k<0时,k+
,构造辅助函数,求导根据函数的单调性求得函数的极值及最值,利用基本不等式的性质,当k<0时,k+ ![]() ≤﹣2直线y=k+
≤﹣2直线y=k+ ![]() ,与曲线y=g(x)至多有两个交点,当k>0时,k+
,与曲线y=g(x)至多有两个交点,当k>0时,k+ ![]() ≥2>
≥2> ![]() =g(x)极大 , 直线y=k+
=g(x)极大 , 直线y=k+ ![]() ,与曲线y=g(x)只有一个交点,即可求证方程至多有两个实根.
,与曲线y=g(x)只有一个交点,即可求证方程至多有两个实根.
【考点精析】解答此题的关键在于理解函数的极值与导数的相关知识,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了引导居民合理用水,居民生活用水实行二级阶梯水价计量办法,具体如下:第一阶梯,每户居民月用水量不超过12吨,价格为4元/吨;第二阶梯,每户居民月用水量超过12吨,超过部分的价格为8元/吨.为了了解全市居民月用水量的分布情况,通过抽样获得了100户居民的月用水量(单位:吨),将数据按照[0,2],(2,4],…,(14,16]分成8组,制成了如图1所示的频率分布直方图.

(Ⅰ)求频率分布直方图中字母a的值,并求该组的频率;
(Ⅱ)通过频率分布直方图,估计该市居民每月的用水量的中位数m的值(保留两位小数);
(Ⅲ)如图2是该市居民张某2016年1~6月份的月用水费y(元)与月份x的散点图,其拟合的线性回归方程是 =2x+33,若张某2016年1~7月份水费总支出为312元,试估计张某7月份的用水吨数.
=2x+33,若张某2016年1~7月份水费总支出为312元,试估计张某7月份的用水吨数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,AB=DP=2
 ,E为CD的中点,点F在线段PB上.
,E为CD的中点,点F在线段PB上. 
(Ⅰ)求证:AD⊥PC;
(Ⅱ)当三棱锥B﹣EFC的体积等于四棱锥P﹣ABCD体积的 时,求
时,求  的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=x+m与抛物线x2=4y相切,且与x轴的交点为M,点N(﹣1,0).若动点P与两定点M,N所构成三角形的周长为6.
(Ⅰ)求动点P的轨迹C的方程;
(Ⅱ) 设斜率为 的直线l交曲线C于A,B两点,当PN⊥MN时,证明:∠APN=∠BPN.
的直线l交曲线C于A,B两点,当PN⊥MN时,证明:∠APN=∠BPN. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.若直线l的极坐标方程为
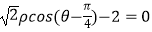 ,曲线C的极坐标方程为:ρsin2θ=cosθ,将曲线C上所有点的横坐标缩短为原来的一半,纵坐标不变,然后再向右平移一个单位得到曲线C1 . (Ⅰ)求曲线C1的直角坐标方程;
,曲线C的极坐标方程为:ρsin2θ=cosθ,将曲线C上所有点的横坐标缩短为原来的一半,纵坐标不变,然后再向右平移一个单位得到曲线C1 . (Ⅰ)求曲线C1的直角坐标方程;
(Ⅱ)已知直线l与曲线C1交于A,B两点,点P(2,0),求|PA|+|PB|的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|2x﹣a|+|2x﹣1|,a∈R. (I)当a=3时,求关于x的不等式f(x)≤6的解集;
(II)当x∈R时,f(x)≥a2﹣a﹣13,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】过双曲线x2﹣
 =1的右支上一点P,分别向圆C1:(x+4)2+y2=4和圆C2:(x﹣4)2+y2=1作切线,切点分别为M,N,则|PM|2﹣|PN|2的最小值为( )
=1的右支上一点P,分别向圆C1:(x+4)2+y2=4和圆C2:(x﹣4)2+y2=1作切线,切点分别为M,N,则|PM|2﹣|PN|2的最小值为( )
A.10
B.13
C.16
D.19
相关试题

