【题目】己知⊙O的半径为 ，弦AB=2，以AB为底边，在圆内画⊙0的内接等腰△ABC，则底边AB边上的高CD长为（ ）
A. +1
B. ﹣1
C. 或 ﹣1
D. +1或 +1

参考答案：

【答案】C
【解析】如图1，连接OA，

∵AC=BC= AB=1，CD⊥AB，

∴AD=BD，CD过圆心，

∴OD= =1，

∴CD=OC+OD=1+ ，

如图2，连接OA，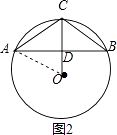

∵AC=BC= AB=1，CD⊥AB，

∴AD=BD，CD过圆心，

∴OD= =1，

∴CD=OC﹣OD= ﹣1，

综上所述： 1或 1．

所以答案是：C．

【考点精析】关于本题考查的勾股定理的概念和垂径定理，需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧才能得出正确答案．

关闭