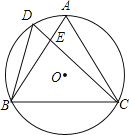
【题目】如图,D是正△ABC的外接圆⊙O上弧AB上一点,给出下列结论:①∠BDC=∠ADC=60°;②AEBE=CEED;③CA2=CECD;④CD=BD+AD.其中正确的个数是( )
A.4 B.3 C.2 D.1
参考答案:
【答案】A
【解析】
试题分析:连接AD,根据等边三角形的性质得到∠BAC=∠ABC=60°,由圆周角定理得到∠BDC=∠BAC=60°,∠ADC=∠ABC=60°,于是得到∠BDC=∠ADC=60°,故①正确;根据圆周角定理得到∠D=∠A,∠ABD=∠ACD,推出△BDE∽△ACE,根据相似三角形的性质即可得到AEBE=CEED;故②正确;由于∠ADC=∠EAC=60°,∠ACE=∠ACD,得到△ACD∽△ACE,根据相似三角形的性质得到CA2=CECD;故③正确;在CD上截取CF=BD,通过△ABD≌△ACF,得到AD=AF,推出△ADF是等边三角形,得到DF=AD,等量代换即可得到结论.
解:连接AD,∵△ABC是等边三角形,
∴∠BAC=∠ABC=60°,
∴∠BDC=∠BAC=60°,∠ADC=∠ABC=60°,
∴∠BDC=∠ADC=60°,故①正确;
∵∠D=∠A,∠ABD=∠ACD,
∴△BDE∽△ACE,
∴![]() ,
,
∴AEBE=CEED;故②正确;
∵∠ADC=∠EAC=60°,∠ACE=∠ACD,
∴△ACD∽△ACE,
∴![]() ,
,
∴CA2=CECD;故③正确;
在CD上截取CF=BD,
在△ABD与△ACF中,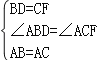 ,
,
∴△ABD≌△ACF,
∴AD=AF,
∵∠ADC=60°,
∴△ADF是等边三角形,
∴DF=AD,
∵CD=CF+DF,
∴CD=BD+AD.故④正确.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市1月1日的最高气温是7C,最低气温是–2C,则这一天的温差是( )
A. 5C B. –5C C. 9C D. 10C
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店盈利80元,记作+80元,那么亏损50元记作__________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙M交x轴于A(﹣1,0),B(3,0)两点.交y轴于C(0,3),D(0,1)两点.
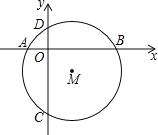
(1)求点M的坐标;
(2)求弧BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点(其中P、Q不与端点重合),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,下列结论:(1)BP=CM;(2)△ABQ≌△CAP;(3)∠CMQ的度数始终等于60°;(4)当第
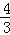 秒或第
秒或第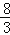 秒时,△PBQ为直角三角形.其中正确的结论有( )
秒时,△PBQ为直角三角形.其中正确的结论有( )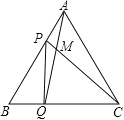
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣3、0、4、0.5这四个数中最小的数是( ).
A.﹣3 B.0.5 C.0 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】把“对顶角相等”改写成“如果……那么……”的形式是__________________.
相关试题

