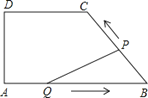
【题目】如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t s,解答下列问题:
(1)当t为何值时,P,Q两点同时停止运动?
(2)设△PQB的面积为S,当t为何值时,S取得最大值,并求出最大值;
(3)当△PQB为等腰三角形时,求t的值.
参考答案:
【答案】(1)、5;(2)、![]() ;(3)、t=
;(3)、t=![]() s,
s,![]() s或t=4s
s或t=4s
【解析】试题分析:(1)、通过比较线段AB,BC的大小,找出较短的线段,根据速度公式可以直接求得;(2)、由已知条件,把△PQB的边QB用含t的代数式表示出来,三角形的高可由相似三角形的性质也用含t的代数式表示出来,代入三角形的面积公式可得到一个二次函数,即可求出S的最值;(3)、根据等腰三角形的性质和余弦公式列出等式求解,即可求的结论.
试题解析:(1)、作CE⊥AB于E, ∵DC∥AB,DA⊥AB, ∴四边形AECD是矩形,
∴AE=CD=5,CE=AD=4, ∴BE=3, ∴BC=5, ∴BC<AB,
∴P到C时,P、Q同时停止运动, ∴t=![]() (秒), 即t=5秒时,P,Q两点同时停止运动.
(秒), 即t=5秒时,P,Q两点同时停止运动.
(2)、由题意知,AQ=BP=t, ∴QB=8﹣t, 作PF⊥QB于F,则△BPF~△BCE,
∴![]() ,即
,即![]() , ∴BF=
, ∴BF=![]() ,
,![]()
∴S=![]() QBPF=
QBPF=![]() ×
×![]() (8﹣t)=﹣
(8﹣t)=﹣![]() (t﹣4)2+
(t﹣4)2+![]() (0<t≤5),
(0<t≤5),
∵﹣![]() <0, ∴S有最大值,当t=4时,S的最大值是
<0, ∴S有最大值,当t=4时,S的最大值是![]() ;
;
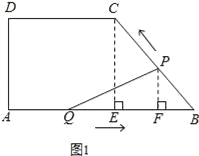
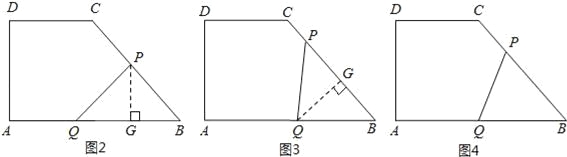
(3)、∵cos∠B=![]() , ①当PQ=PB时(如图2所示),则BG=
, ①当PQ=PB时(如图2所示),则BG=![]() BQ,
BQ,![]() =
=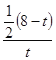 =
=![]() ,解得t=
,解得t=![]() s,
s,
②当PQ=BQ时(如图3所示),则BG=![]() PB,
PB,![]() =
=![]() =
=![]() ,解得t=
,解得t=![]() s,
s,
③当BP=BQ时(如图4所示),则8﹣t=t, 解得:t=4.
综上所述:当t=![]() s,
s,![]() s或t=4s时,△PQB为等腰三角形.
s或t=4s时,△PQB为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解4x2+12xy+9y2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=90°,∠BOC=30°,射线OM平分∠AOC,ON平分∠BOC.
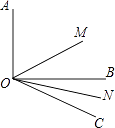
(1)求∠MON的度数;
(2)如果(1)中,∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中,∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)、(2)、(3)的结果中,你能看出什么规律? -
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个在三视图中俯视图与主视图完全相同的几何体 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一张比例尺为1:5000000的地图上,甲、乙两地相距70毫米,此两地的实际距离为( )
A.3.5千米
B.35千米
C.350千米
D.3500千米 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.x2+x2=2x4B.x3x2=x5C.x9÷x3=x3D.(x2)3=x5
-
科目: 来源: 题型:
查看答案和解析>>【题目】农大毕业的小王回乡自主创业,在大棚中栽培新品种的蘑菇,该种蘑菇在18℃的条件下生长最快,因此用装有恒温系统的大棚栽培,每天只开启一次,如图是某天恒温系统从开启升温到保持恒温及关闭.大棚内温度y(℃)随时间x(时)变化的函数图象,其中BC段是函数y=
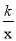 (k>0)图象的一部分.若该蘑菇适宜生长的温度不低于12℃,则这天该种蘑菇适宜生长的时间为( )
(k>0)图象的一部分.若该蘑菇适宜生长的温度不低于12℃,则这天该种蘑菇适宜生长的时间为( )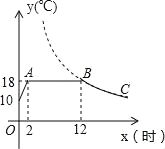
A.18小时 B.17.5小时 C.12小时 D.10小时
相关试题

