【题目】如图,直角三角板ABC的斜边AB=12cm,∠A=30°,将三角板ABC绕点C顺时针旋转90°至三角板A′B′C′的位置后,再沿CB方向向左平移,使点B′落在原三角板ABC的斜边AB上,则三角板A′B′C′平移的距离为( )
A.6cm
B.(6﹣2![]() )cm
)cm
C.3cm
D.(4![]() ﹣6)cm
﹣6)cm
参考答案:
【答案】B
【解析】解:∵AB=12cm,∠A=30°,
∴BC=![]() AB=
AB=![]() ×12=6cm,
×12=6cm,
由勾股定理得,AC=![]() =
=![]() =6
=6![]() cm,
cm,
∵三角板ABC绕点C顺时针旋转90°得到三角板A′B′C′,
∴B′C′=BC=6cm,
∴AB′=AC﹣B′C′=6![]() ﹣6,
﹣6,
过点B′作B′D⊥AC交AB于D,
则B′D=![]() AB′=
AB′=![]() ×(6
×(6![]() ﹣6)=(6﹣2
﹣6)=(6﹣2![]() )cm.
)cm.
故选B.
【考点精析】本题主要考查了平移的性质的相关知识点,需要掌握①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>b,用“>”号或“<”号连接:a+3________b+3,b-a_________0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年我市某公司分两次采购了一批大蒜,第一次花费40万元,第二次花费60万元,已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元,第二次采购时每吨大蒜的价格比去年的平均价格下降了500元,第二次采购的数量是第一次采购数量的两倍.
(1)试问去年每吨大蒜的平均价格是多少元?
(2)该公司可将大蒜加工成蒜粉或蒜片,若单独加工成蒜粉,每天可加工8吨大蒜,每吨大蒜获利1000元;若单独加工成蒜片,每天可加工12吨大蒜,每吨大蒜获利600元.为出口需要,所有采购的大蒜必须在30天内加工完毕,且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半.为获得最大利润,应将多少吨大蒜加工成蒜粉?最大利润为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2,正确的个数为

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为4的正方形ABCD的对称中心是坐标原点O,AB∥
 轴,BC∥
轴,BC∥  轴,反比例函数
轴,反比例函数  与
与  的图像均与正方形ABCD的边相交,则图中阴影部分的面积之和是( )
的图像均与正方形ABCD的边相交,则图中阴影部分的面积之和是( )
A.2
B.4
C.6
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知坐标平面上的机器人接受指令“[a , A]”(a≥0,0°<A<180°)后的行动结果为:在原地顺时针旋转A后,再向面对方向沿直线行走a.若机器人的位置在原点,面对方向为y轴的负半轴,则它完成一次指令[2,60°]后,所在位置的坐标为( )
A.(-1,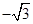 )
)
B.(-1,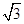 )
)
C.(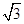 ,-1)
,-1)
D.(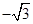 ,-1)
,-1) -
科目: 来源: 题型:
查看答案和解析>>【题目】有四根细木棒,长度分别为 3cm、5cm、7cm、9cm,以其中任意三条为边可以构成个三角形.
相关试题

