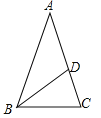
【题目】如图，在△ABC中，AB=AC=1，BC=，在AC边上截取AD=BC，连接BD．

（1）通过计算，判断与ACCD的大小关系；

（2）求∠ABD的度数．

参考答案：

【答案】（1）；（2）36°．

【解析】

试题分析：（1）先求得AD、CD的长，然后再计算出与ACCD的值，从而可得到与ACCD的关系；

（2）由（1）可得到=ACCD，然后依据对应边成比例且夹角相等的两三角形相似证明△BCD∽△ABC，依据相似三角形的性质可知∠DBC=∠A，DB=CB，然后结合等腰三角形的性质和三角形的内角和定理可求得∠ABD的度数．

试题解析：（1）∵AD=BC=，∴==．

∵AC=1，∴CD==，∴；

（2）∵，∴，即，又∵∠C=∠C，∴△ABC∽△BDC，∴，又∵AB=AC，∴BD=BC=AD，∴∠A=∠ABD，∠ABC=∠C=∠BDC．

设∠A=∠ABD=x，则∠BDC=∠A+∠ABD=2x，∴∠ABC=∠C=∠BDC=2x，∴∠A+∠ABC+∠C=x+2x+2x=180°，解得：x=36°，∴∠ABD=36°．

关闭