【题目】如图,在平面直角坐标系中,点A的坐标为(2,3)且AO=BO,∠AOB=90°则点B的坐标为( )

A.(2,3)B.(-3,2)C.(-3,-2)D.(-2,3)
参考答案:
【答案】B
【解析】
过A作AC⊥x轴,垂足为C,作BD⊥x轴垂足为D.证明△AOC和△BOD全等,那么B的横坐标就是OD长的相反数,B的纵坐标就是OC长的绝对值,由此可得出B的坐标.
解:作AC⊥x轴,垂足为C,作BD⊥x轴垂足为D.

则∠ACO=∠ODB=90°,
∴∠AOC+∠OAC=90°.
又∵∠AOB=90°,
∴∠AOC+∠BOD=90°
∴∠OAC=∠BOD.
在△ACO和△ODB中
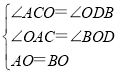
∴△ACO≌△ODB(AAS).
∴OD=AC=3,DB=OC=2.
∴点B的坐标为(-3,2).
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下列方程.
(1)(6x-1)2-25=0; (2)(3x-2)2=x2;
(3)x2+
 =
= x; (4)(x+1)(x-1)+2(x+3)=8.
x; (4)(x+1)(x-1)+2(x+3)=8. -
科目: 来源: 题型:
查看答案和解析>>【题目】某博物馆每周都吸引大量中外游客前来参观,如果游客过多,对馆中的珍贵文物会产生不利影响,但同时考虑到文物的修缮和保存费用问题,还要保证一定的门票收入,因此,博物馆采取了涨浮门票价格的方法来控制参观人数,在该方法实施过程中发现:每周参观人数与票价之间存在着如图所示的一次函数关系.在这种情况下,如果要保证每周
 万元的门票收入,那么每周应限定参观人数是多少?门票价格应是多少.
万元的门票收入,那么每周应限定参观人数是多少?门票价格应是多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图AD是△ABC的角平分线,DF⊥AB,垂足为F,如图DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积( )

A.6B.12C.8D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,
 ,
, 的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,
的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点, ,垂足为G,若
,垂足为G,若 ,则AE的边长为
,则AE的边长为


A.
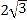 B.
B.  C. 4 D. 8
C. 4 D. 8 -
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。

(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
相关试题

