【题目】已知,二次函数![]() ≠0
≠0![]() 的图像经过点(3,5)、(2,8)、(0,8).
的图像经过点(3,5)、(2,8)、(0,8).
①求这个二次函数的解析式;
②已知抛物线![]() ≠0
≠0![]() ,
,![]() ≠0
≠0![]() ,且满足
,且满足![]() ≠0,1
≠0,1![]() ,则我们称抛物线
,则我们称抛物线![]() 互为“友好抛物线”,请写出当
互为“友好抛物线”,请写出当![]() 时第①小题中的抛物线的友好抛物线,并求出这“友好抛物线”的顶点坐标.
时第①小题中的抛物线的友好抛物线,并求出这“友好抛物线”的顶点坐标.
参考答案:
【答案】(1)![]() ;(2)(1,-18)或(1,
;(2)(1,-18)或(1,![]() )
)
【解析】(1)先把三个点的坐标的人y=ax2+bx+c=0(a≠0)得到关于a、b、c的方程组,然后解方程组求出a、b、c 的值;
(2)根据图中的定义得到![]() =
=![]() =
=![]() =-
=-![]() 或
或![]() =
=![]() =
=![]() =-
=-![]() ,则可得到友好抛物线的解析式是:y=2x2-4x-16或y=
,则可得到友好抛物线的解析式是:y=2x2-4x-16或y=![]() x2-x-4,然后分别配成顶点式,则可得到它们的顶点坐标.
x2-x-4,然后分别配成顶点式,则可得到它们的顶点坐标.
解:(1)根据题意,得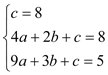 可以解得
可以解得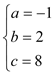 ,
,
∴这个抛物线的解析式是![]() .
.
(2)根据题意,得![]() 或
或![]()
解得a2=2,b2=-4,c2=-16或a1=![]() ,b1=-1,c1=-4,,
,b1=-1,c1=-4,,
友好抛物线的解析式是:y=2x2-4x-16或y=![]() x2-x-4,
x2-x-4,
∴它的顶点坐标是(1,-18)或(1,![]() )
)
“点睛”二次函数是初中数学的一个重要内容之一,其中解析式的确定一般都采用待定系数法求解,但是要求学生根据给出的已知条件的不同,要能够恰当地选取合适的二次函数解析式的形式,选择得当则解题简捷,若选择不得当,就会增加解题的难度。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3).
(1)求△AOB的面积;
(2)点P在x轴上,当PA+PB的值最小时,在图中画出点P,并求出点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2
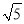 ,反比例函数y=
,反比例函数y=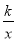 的图象经过点B,则k的值为______.
的图象经过点B,则k的值为______.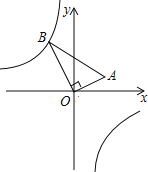
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(﹣2,a),B(1,b)是一次函数y=﹣2x+1图象上的两个点,则a与b的大小关系是( )
A.a>bB.a<bC.a=bD.不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句中正确的是( )
A. 圆周角的度数等于它所对弧的度数的一半 B. 三点确定一个圆
C. 圆有四条对称轴 D. 各边相等的多边形是正多边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a+2的相反数是﹣5,则a=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为3cm,OP=4cm,则点P与⊙O的位置关系是( )
A. 点P在圆内 B. 点P在圆上 C. 点P在圆外 D. 无法确定
相关试题

