【题目】已知f(x)是定义在(0,+∞)上的单调函数,且对任意的x∈(0,+∞),都有f[f(x)﹣log2x]=3,则方程f(x)﹣f′(x)=2的解所在的区间是( )
A.(0, ![]() )
)
B.( ![]() ,1)
,1)
C.(1,2)
D.(2,3)
参考答案:
【答案】C
【解析】解:根据题意,对任意的x∈(0,+∞),都有f[f(x)﹣log2x]=3, 又由f(x)是定义在(0,+∞)上的单调函数,
则f(x)﹣log2x为定值,
设t=f(x)﹣log2x,则f(x)=log2x+t,
又由f(t)=3,即log2t+t=3,
解可得,t=2;
则f(x)=log2x+2,f′(x)= ![]() ,
,
将f(x)=log2x+2,f′(x)= ![]() 代入f(x)﹣f′(x)=2,
代入f(x)﹣f′(x)=2,
可得log2x+2﹣ ![]() =2,
=2,
即log2x﹣ ![]() =0,
=0,
令h(x)=log2x﹣ ![]() ,
,
分析易得h(1)=﹣ ![]() <0,h(2)=1﹣
<0,h(2)=1﹣ ![]() >0,
>0,
则h(x)=log2x﹣ ![]() 的零点在(1,2)之间,
的零点在(1,2)之间,
则方程log2x﹣ ![]() =0,即f(x)﹣f′(x)=2的根在(1,2)上,
=0,即f(x)﹣f′(x)=2的根在(1,2)上,
故选C.
根据题意,由单调函数的性质,可得f(x)﹣log2x为定值,可以设t=f(x)﹣log2x,则f(x)=log2x+t,又由f(t)=3,即log2t+t=3,解可得t的值,可得f(x)的解析式,对其求导可得f′(x);将f(x)与f′(x)代入f(x)﹣f′(x)=2,变形化简可得log2x﹣ ![]() =0,令h(x)=log2x﹣
=0,令h(x)=log2x﹣ ![]() ,由二分法分析可得h(x)的零点所在的区间为(1,2),结合函数的零点与方程的根的关系,即可得答案.
,由二分法分析可得h(x)的零点所在的区间为(1,2),结合函数的零点与方程的根的关系,即可得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.若a∈R,则“ <1”是“a>1”的必要不充分条件
<1”是“a>1”的必要不充分条件
B.“p∧q为真命题”是“p∨q为真命题”的必要不充分条件
C.若命题p:“?x∈R,sinx+cosx≤ ”,则¬p是真命题
”,则¬p是真命题
D.命题“?x0∈R,使得x02+2x0+3<0”的否定是“?x∈R,x2+2x+3>0” -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 ,向量
,向量  如图表示,则( )
如图表示,则( ) 
A.?λ>0,使得
B.?λ>0,使得< ,
,  >=60°
>=60°
C.?λ<0,使得< ,
,  >=30°
>=30°
D.?λ>0,使得 为不为0的常数)
为不为0的常数) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Acos2(x+φ)+1(A>0,>0,0<φ<
 )的最大值为3,f(x)的图象与y轴的交点坐标为(0,2),其相邻两条对称轴间的距离为2,则f(1)+f(2)+f(3)+…+f(2016)的值为( )
)的最大值为3,f(x)的图象与y轴的交点坐标为(0,2),其相邻两条对称轴间的距离为2,则f(1)+f(2)+f(3)+…+f(2016)的值为( )
A.2468
B.3501
C.4032
D.5739 -
科目: 来源: 题型:
查看答案和解析>>【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在数列{an}中,a1=4,an>0,前n项和为Sn , 若
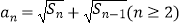 .
.
(1)求数列{an}的通项公式;
(2)若数列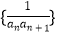 的前n项和为Tn , 求Tn .
的前n项和为Tn , 求Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”,为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研,人社部从网上年龄在15~65岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下

年龄
[15,25)
[25,35)
[35,45)
[45,55)
[55,65]
支持“延迟退休”的人数
15
5
15
28
17
(1)由以上统计数据填2×2列联表,并判断是否95%的把握认为以45岁为界点的不同人群对“延迟退休年龄政策”的支持有差异;45岁以下
45岁以上
总计
支持
不支持
总计
(2)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动,现从这8人中随机抽2人. ①抽到1人是45岁以下时,求抽到的另一人是45岁以上的概率;
②记抽到45岁以上的人数为X,求随机变量X的分布列及数学期望.P(K2≥k0)
0.100
0.050
0.010
0.001
k0
2.706
3.841
6.635
10.828
 .
.
相关试题

