【题目】如图,△ABC是等边三角形,BD是AC边上的高,延长BC至E,使CE=CD,连接DE。

(1)求∠E的度数?
(2)△DBE是什么三角形?为什么?
参考答案:
【答案】(1)30°,(2)△DBE是等腰三角形.理由见解析
【解析】
(1)由题意可推出∠ACB=60°,∠E=∠CDE,然后根据三角形外角的性质可知:∠ACB=∠E+∠CDE,即可推出∠E的度数;
(2)根据等边三角形的性质可知,BD不但为AC边上的高,也是∠ABC的角平分线,即得:∠DBC=30°,然后再结合(1)中求得的结论,即可推出△DBE是等腰三角形.
(1)∵△ABC是等边三角形,
∴∠ACB=60°,
∵CD=CE,
∴∠E=∠CDE,
∵∠ACB=∠E+∠CDE,
∴∠E=![]() ∠ACB=
∠ACB=![]() ×60°=30°,
×60°=30°,
(2)∵△ABC是等边三角形,BD⊥AC,
∴∠ABC=60°,
∴∠DBC=![]() ∠ABC=30°,
∠ABC=30°,
∵∠E=30°,
∴∠DBC=∠E,
∴△DBE是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 中,
中, 厘米,
厘米, 厘米,点D为AB的中点.如果点P在线段BC上以v厘米/秒的速度由B点向C点运动.同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为3厘米/秒,则当
厘米,点D为AB的中点.如果点P在线段BC上以v厘米/秒的速度由B点向C点运动.同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为3厘米/秒,则当 与
与 全等时,v的值为______
全等时,v的值为______
-
科目: 来源: 题型:
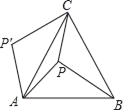
查看答案和解析>>【题目】如图,P是等边△ABC内一点,且PA=6,PC=8,PB=10,若△APB绕点A逆时针旋转60°后,得到△AP′C,则∠APC=_____°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点0出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P2016的坐标为_____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将两块大小相同的含30°角的直角三角板(∠BAC=∠B1A1C=30°)按图①的方式放置,固定三角板A1B1C,然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90°)至图②所示的位置,AB与A1C交于点E,AC与A1B1交于点F,AB与A1B1交于点O.

(1)求证:△BCE≌△B1CF.
(2)当旋转角等于30°时,AB与A1B1垂直吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知
 是等腰直角三角形,
是等腰直角三角形, ,点D是BC的中点
,点D是BC的中点 作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG. 试猜想线段BG和AE的数量关系是______;
试猜想线段BG和AE的数量关系是______; 将正方形DEFG绕点D逆时针方向旋转
将正方形DEFG绕点D逆时针方向旋转 ,
, 判断
判断 中的结论是否仍然成立?请利用图2证明你的结论;
中的结论是否仍然成立?请利用图2证明你的结论; 若
若 ,当AE取最大值时,求AF的值.
,当AE取最大值时,求AF的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC。

(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BCD的度数。
相关试题

