【题目】如图,△ABC为等边三角形,D为BC延长线上的一点,以AD为边向形外作等边△ADE,连接CE.(1) 求证:△ACE≌△ABD;
(2) 在点D运动过程中,∠DCE的度数是否发生变化?若不变化,求它的度数;若变化,说明理由;
(3) 若∠BAE=150°,△ABD的面积为6,求四边形ACDE的面积.
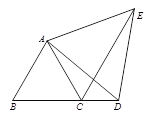
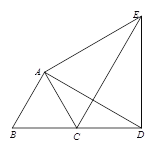
备用图
参考答案:
【答案】(1)证明见解析;(2)不发生变化,理由见解析;(3)12
【解析】试题分析:(1)易证AB=AC=BC,AD=AE,∠BAC=∠DAE=60°,即可求得∠BAD=∠CAE,由全等三角形的判定SAS,证明△ABD≌△ACE;
(2)根据(1)知△ACE≌△ABD,然后根据全等三角形的性质和等边三角形性质,得出∠DCE=60°,得出不发生变化;
(3)根据(1)的结论,由∠BAE=150°,得到△ACE,△DCE,△ABD的面积相等,从而求出四边形的面积.
试题解析:(1) ∵△ABC为等边三角形,△ADE为等边三角形,∴∠ABC=∠ACB=60°,∠BAC=∠DAE=60°,AB=AC,AD=AE,∴∠BAC+∠DAC=∠DAC+∠DAE,即∠BAD=∠CAE.在△ACE与△ABD中,AB=AC,∠BAD=∠CAE,AD=AE,∴△ACE≌△ABD;
(2) 在点D运动过程中,∠DCE的度数不发生变化.理由如下:由(1)知:△ACE≌△ABD,∴∠ABC=∠ACE=60°.∵∠ACB=60°,∴∠ACD=120°,∠DCE=60°,∴在点D运动过程中,∠DCE的度数不发生变化.
(3)∵△ABC和△ADE是等边三角形
∴∠BAC=∠DAE=60°
∵∠BAE=150°
∴∠CAD=30°,∠BAD=90°,
∴∠BAD=30°
即△ACE≌△DCE
∵△ABD≌△ACE
∴四边形ACDE的面积=2△ACD的面积=2△ABD的面积=2×6=12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠ABC=90°,BD的垂直平分线交AC、BD分别于点M、N,点M为AC中点.
(1) 求证:AM=DM;
(2) 求∠ADC的度数;
(3) 当∠BCD为_______°时,∠BMD为120°.(直接写出结果)
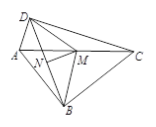
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果圆锥的底面半径为2,母线长为6,那么这个圆锥的侧面积是
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.x3+x2=x5
B.x3﹣x2=x
C.(x3)2=x5
D.x3÷x2=x -
科目: 来源: 题型:
查看答案和解析>>【题目】下列句子中,不是命题的是( )
A. 三角形的内角和等于180度 B. 对顶角相等
C. 过一点作已知直线的平行线 D. 两点确定一条直线
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( )
A.周长相等的锐角三角形都全等
B.周长相等的等腰直角三角形都全等
C.周长相等的钝角三角形都全等
D.周长相等的直角三角形都全等 -
科目: 来源: 题型:
查看答案和解析>>【题目】在社会实践活动中,某中学对甲、乙,丙、丁四个超市三月份的苹果价格进行调查.它们的价格的平均值均为3.50元,方差分别为S甲2=0.3,S乙2=0.4,S丙2=0.1,S丁2=0.25.三月份苹果价格最稳定的超市是( )
A.甲
B.乙
C.丙
D.丁
相关试题

