【题目】已知,△ABC、△DCE均为等边三角形,且B、C、E三点在一条直线上,BD与AE相交于O点.
(1)求证:△BCD≌△ACE;
(2)求∠DOE的度数;
(3)连接MN,求证:MN∥BE.

参考答案:
【答案】见解析
【解析】试题分析:
(1) △ABC、△DCE均为等边三角形,易知BC=AC,CD=CE. 这样,对于△BCD与△ACE而言,已经获得了两组对应边的相等关系,只要再证明这两组对应边所夹的角∠BCD与∠ACE对应相等就可以用SAS证明这组三角形全等了.观察图形可知,∠BCD与∠ACE均是由等边三角形的一个内角加上一个相同的角∠ACD而形成的,进而可以证明其相等.
(2) 观察图形可知,∠DOE是△BOE的一个外角,容易联想到用三角形外角的相关结论求解该题. 利用三角形外角的相关结论以及第(1)小题中的全等三角形,可以将∠DOE转化为∠DBC+∠BDC,再由三角形外角的相关结论可知∠DOE与等边三角形内角∠DCE相等,得到答案.
(3) 分析条件可知∠ACN=60°,结合图形的形状可以猜想△MCN为等边三角形. 若△MCN为等边三角形,即可通过“内错角相等,两直线平行”的方法证明MN∥BE. 本题的问题转化为如何证明△MCN为等边三角形. 利用第(1)小题中的全等三角形可以证明△CAN与△CBM全等,得到CN=CM. 这样就证明了△MCN为等边三角形,进而容易证明MN∥BE.
试题解析:
(1) ∵△ABC与△DCE均为等边三角形,
∴BC=AC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠ACD =∠DCE+∠ACD,即∠BCD=∠ACE,
∵在△BCD与△ACE中:
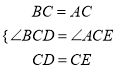 ,
,
∴△BCD≌△ACE (SAS).
(2) ∵∠DOE是△BOE的一个外角,
∴∠DOE=∠OBE+∠OEB,即∠DOE=∠DBC+∠AEC,
∵△BCD≌△ACE,
∴∠BDC=∠AEC,
∴∠DOE=∠DBC+∠BDC,
∵∠DCE是△BCD的一个外角,
∴∠DCE=∠DBC+∠BDC,
∴∠DOE=∠DCE,
∵△DCE为等边三角形,
∴∠DCE=60°,
∴∠DOE=∠DCE=60°.
(3) ∵△ABC与△DCE均为等边三角形,
∴AC=BC,∠ACB=∠DCE=60°,即∠BCM=∠ECN=60°,
∵B、C、E三点在一条直线上,
∴∠ACN+∠BCM+∠ECN=180°,
∴∠ACN=180°-∠BCM-∠ECN=180°-60°-60°=60°,
∴∠ACN=∠BCM,
∵△BCD≌△ACE,
∴∠CBD=∠CAE,即∠CAN=∠CBM,
∵在△CAN与△CBM中:
 ,
,
∴△CAN≌△CBM (ASA),
∴CN=CM,
∵∠ACN=60°且CN=CM,
∴△MCN为等边三角形,
∴∠CMN=60°,
∴∠CMN=∠ACB=60°,
∴MN∥BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】肥皂泡的泡壁厚度大约是0.0007mm,0.0007用科学记数法表示为( )
A.0.7×10﹣3
B.7×10﹣3
C.7×10﹣4
D.7×10﹣5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系式 ;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)
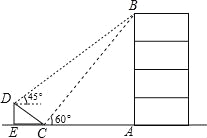
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,在“4×4”正方形网格中,已有2个小正方形被涂黑.请你分别在下面2张图中再将若干个空白的小正方形涂黑,使得涂黑的图形成为轴对称图形.(图(1)要求只有1条对称轴,图(2)要求只有2条对称轴).

(只有1条对称轴) (只有2条对称轴)
图⑴ 图⑵
⑵如图,A、B为直线MN外两点,且到MN的距离不相等.分别在MN上求一点P,并满足如下条件:①在图⑶中求一点P使得PA+PB最小; ②在图⑷中求一点P使得|PA-PB|最大.
(不写作法,保留作图痕迹)
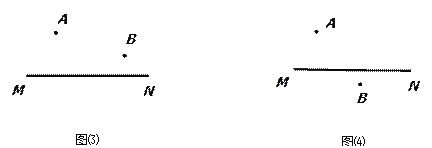
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程4x2+1=4x的根的情况是( )
A.没有实数根B.只有一个实数根
C.有两个相等的实数根D.有两个不相等的实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式x2﹣3kxy﹣3y2+6xy﹣8不含xy项,则k= .
相关试题

