【题目】国家规定,中小学生每天在校体育活动时间不低于1小时,为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t<1,C组:1≤t<1.5,D组:t≥1.5),绘制成如下两幅不完整统计图,请根据图中信息回答问题:
(1)此次抽查的学生数为 人;
(2)补全条形统计图;
(3)从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是 ;
(4)若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有 人.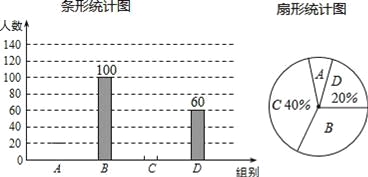
参考答案:
【答案】(1) 300;(2)补全统计图详见解析;(3) 40%;(4) 720.
【解析】试题分析:(1)根据题意即可得到结论;
(2)求出C组的人数,A组的人数补全条形统计图即可;
(3)根据概率公式即可得到结论;
(4)用总人数乘以达到国家规定体育活动时间的百分比即可得到结论.
试题解析:(1)60÷20%=300(人),
答:此次抽查的学生数为300人.
故答案为:300;
(2)C组的人数=300×40%=120(人),
A组的人数=300﹣100﹣120﹣60=20(人),
补全条形统计图如图所示:
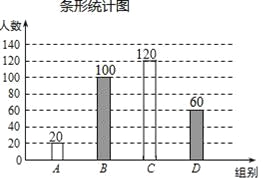
(3)该生当天在校体育活动时间低于1小时的概率是![]() =40%,
=40%,
故答案为:40%;
(4)当天达到国家规定体育活动时间的学生有1200×![]() =720人.
=720人.
故答案为:720人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)(x-1)3+27=0. (2)(x+1)2=81
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于命题“如果a>b>0,那么a2>b2 . ”用反证法证明,应假设( )
A.a2>b2
B.a2<b2
C.a2≥b2
D.a2≤b2 -
科目: 来源: 题型:
查看答案和解析>>【题目】口袋内装有一些除颜色外完全相同的红球、白球和黑球,从中摸出一球,摸出红球的概率是0.2,摸出白球的概率是0.5,那么摸出黑球的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连结BD.
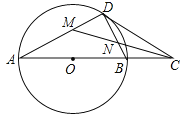
(1)求证:∠A=∠BDC;
(2)若CM平分∠ACD,且分别交AD、BD于点M、N,当DM=1时,求MN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分6分)
(1)(3分)(-3)2-|-
 |+(3.14-x)0
|+(3.14-x)0(2)(4分)先化简,再求值:[(2x-y)2+(2x-y)(2x+y)]÷(4x),其中x=2,y=-1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?

相关试题

