【题目】如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个锐角为60°的菱形,剪口与折痕所成的角a的度数应为 . 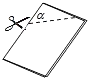
参考答案:
【答案】30°或60°
【解析】解:∵四边形ABCD是菱形, ∴∠ABD= ![]() ∠ABC,∠BAC=
∠ABC,∠BAC= ![]() ∠BAD,AD∥BC,
∠BAD,AD∥BC,
∵∠BAC=60°,
∴∠BAD=180°﹣∠ABC=180°﹣60°=120°,
∴∠ABD=30°,∠BAC=60°.
∴剪口与折痕所成的角a的度数应为30°或60°.
所以答案是30°或60°.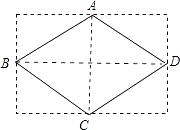
【考点精析】本题主要考查了菱形的性质的相关知识点,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知线段AB=20cm,CD=2cm,线段CD在线段AB上运动,E、F分别是AC、BD的中点.
(1)若AC=4cm,则EF=_________cm.
(2)当线段CD在线段AB上运动时,试判断EF的长度是否发生变化?如果不变请求出EF的长度,如果变化,请说明理由.
(3)我们发现角的很多规律和线段一样,如图②已知
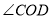 在
在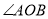 内部转动,OE、OF分别平分
内部转动,OE、OF分别平分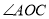 在
在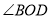 ,则
,则 、
、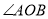 和
和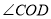 有何关系,请直接写出_______________________.
有何关系,请直接写出_______________________.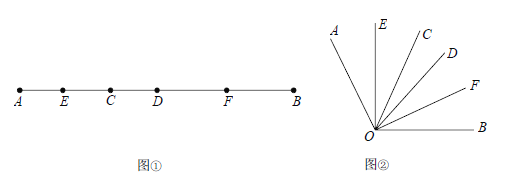
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为12的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G.则BG的长为( )
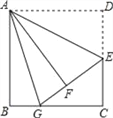
A. 5 B. 4 C. 3 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是( )
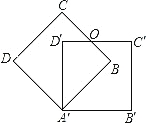
A. 6
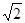 B. 6C. 3
B. 6C. 3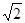 D. 3+3
D. 3+3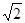
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有【 】个.

A.2 B.3 C.4 D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣11,点B表示10,点C表示18,我们称点A和点C在数轴上相距29个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.

问:(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤∠AGB+∠AED=145°.其中正确的个数是( )

A. 2 B. 3 C. 4 D. 5
相关试题

