Question

【题目】在平面直角坐标系中，长方形OABC的边OC，OA分别在x轴和y轴上，点B的坐标是（5，3），直线y=2x+b与x轴交于点E，与线段AB交于点F．

（1）用含b的代数式表示点E，F的坐标；

（2）当b为何值时，△OFC是等腰三角形；

（3）当FC平分∠EFB时，求点F的坐标．

Answer 1

【答案】（1）E（﹣，0）；（2）①b=﹣2；②b=﹣5；③b=﹣1．（3）F（，3）．

【解析】试题分析：（1）根据B、F两点的纵坐标都是3，即可求出点F的坐标，对于直线y=2x+b，令y=0，求出x，可得点E坐标；

（2）分三种情形：①FO=FC．②OF=OC．③CF=OC分别求解即可；

（3）由AB∥OC，CF平分∠EFB，推出∠BFC=∠FCE=∠EFC，推出EF=EC，由此构建方程即可解决问题；

试题解析：解：（1）∵四边形OABC是矩形，∴BF∥OC．∵B（5，3），∴点F的纵坐标为3，∴3=2x+b，∴x=，∴F（，3），对于直线y=2x+b，令y=0，得到x=﹣，∴E（﹣，0）．

（2）①当FO=FC时，OF=AB=，∴=，∴b=﹣2．

②当OF=OC时，AF==4，∴=4，∴b=﹣5．

③当CF=OC时，FB=4，AF=1，∴=1，∴b=﹣1．

（3）如图，连接CF．

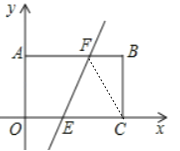
∵AB∥OC，CF平分∠EFB，∴∠BFC=∠FCE=∠EFC，∴EF=EC，∴EF2=EC2．∵F（，3），E（﹣，0），∴32+（+）2=（5+）2，∴b=﹣10+3或﹣10﹣3（舍弃），∴F（，3）．