【题目】计算:
(1)![]() +(﹣1)2017﹣(
+(﹣1)2017﹣(![]() ﹣
﹣![]() ),
),
(2)2(3a2b﹣2ab2)﹣3(ab2+2a2b),
(3)﹣7x2y﹣3xy2+5x2y+13xy,其中x=﹣![]() ,y=
,y=![]()
参考答案:
【答案】(1)- ![]() ;(2)﹣7ab2;(3)﹣
;(2)﹣7ab2;(3)﹣![]() .
.
【解析】
(1)直接利用有理数的加减运算法则计算得出答案;(2)直接去括号进而合并同类项得出答案;(3)直接合并同类项进而把已知代入求出答案.
(1)![]() +(﹣1)2017﹣(
+(﹣1)2017﹣(![]() ﹣
﹣![]() )
)
=![]() ﹣1﹣
﹣1﹣![]() +
+![]()
=![]() +
+![]() ﹣1﹣
﹣1﹣![]()
=1﹣1﹣![]()
=﹣![]() ;
;
(2)2(3a2b﹣2ab2)﹣3(ab2+2a2b)
=6a2b﹣4ab2﹣3ab2﹣6a2b
=﹣7ab2;
(3)﹣7x2y﹣3xy2+5x2y+13xy,
=﹣2x2y﹣3xy2+13xy
把x=﹣![]() ,y=
,y=![]() 代入上式可得:
代入上式可得:
原式=﹣2×(﹣![]() )2×
)2×![]() ﹣3×(﹣
﹣3×(﹣![]() )×(
)×(![]() )2+13×(﹣
)2+13×(﹣![]() )×
)×![]()
=﹣![]() +
+![]() ﹣
﹣![]()
=﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AC,AC的垂直平分线MN交AB于D,交AC于E.

(1)若∠A=40°,求∠BCD的度数;
(2)若AE=5,△BCD的周长17,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校计划购买甲、乙两种图书作为“校园读书节”的奖品,已知甲种图书的单价比乙种图书的单价多10元,且购买3本甲种图书和2本乙种图书共需花费130元
(1)甲、乙两种图书的单价分别为多少元?
(2)学校计划购买这两种图书共50本,且投入总经费不超过1200元,则最多可以购买甲种图书多少本?
-
科目: 来源: 题型:
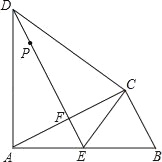
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,以AC为边在△ABC外作等边三角形ACD,过点D作AC的垂线,垂足为F,与AB相交于点E,连接CE.
(1)说明:AE=CE=BE;
(2)若AB=15cm,P是直线DE上的一点.则当P在何处时,PB+PC最小,并求出此时PB+PC的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两座城市的中心火车站A,B两站相距360 km.一列动车与一列特快列车分别从A,B两站同时出发相向而行,动车的平均速度比特快列车快54 km/h,当动车到达B站时,特快列车恰好到达距离A站135 km处的C站.求动车和特快列车的平均速度各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
(1)求证:BD=CE;
(2)求证:∠M=∠N.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是∠AOB的边OA上的一点:
(1)过点P画OB的垂线,垂足为H;
(2)过点H画OA的垂线,交OA于点C;
(3)再看画好垂线的图,你发现了哪个点到哪条直线的距离?分别量一量之后写出来.

相关试题

