【题目】在北京市开展的“首都少年先锋岗”活动中,某数学小组到人民英雄纪念碑站岗执勤,并在活动后实地测量了纪念碑的高度. 方法如下:如图,首先在测量点A处用高为1.5m的测角仪AC测得人民英雄纪念碑MN顶部M的仰角为35°,然后在测量点B处用同样的测角仪BD测得人民英雄纪念碑MN顶部M的仰角为45°,最后测量出A,B两点间的距离为15m,并且N,B,A三点在一条直线上,连接CD并延长交MN于点E. 请你利用他们的测量结果,计算人民英雄纪念碑MN的高度.
(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7)


参考答案:
【答案】人民英雄纪念碑MN.的高度约为36.5米.
【解析】试题分析:由题意得,四边形ACDB,ACEN为矩形,从而得EN=AC=1.5.AB=CD=15,在Rt△MED中,由题意可得ME=DE,设ME=DE=x,则EC=x+15,在Rt△MEC中,可得ME=ECtan∠MCE,从而有x≈0.7(x+15),求出x的值,从而得MN=ME+EN≈36.5 .
试题解析:由题意得,四边形ACDB,ACEN为矩形,
∴EN=AC=1.5,AB=CD=15,
在![]() 中,
中,
∠MED=90°,∠MDE=45°,
∴∠EMD=∠MDE=45°,
∴ME=DE,
设ME=DE=x,则EC=x+15,
在![]() 中,∠MEC=90°,
中,∠MEC=90°,
∠MCE=35°,
∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴人民英雄纪念碑MN.的高度约为36.5米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y = x2 - 4x + 3.
(1)用配方法将y = x2 - 4x + 3化成y = a(x - h)2 + k的形式;
(2)在平面直角坐标系
 中画出该函数的图象;
中画出该函数的图象;(3)当0≤x≤3时,y的取值范围是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
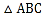 中,
中,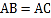 ,D在边AC上,且
,D在边AC上,且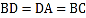 .
.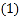 如图1,填空
如图1,填空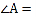 ______
______ ,
,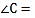 ______
______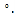
 如图2,若M为线段AC上的点,过M作直线
如图2,若M为线段AC上的点,过M作直线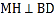 于H,分别交直线AB、BC与点N、E.
于H,分别交直线AB、BC与点N、E. 求证:
求证: 是等腰三角形;
是等腰三角形; 试写出线段AN、CE、CD之间的数量关系,并加以证明.
试写出线段AN、CE、CD之间的数量关系,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB为⊙O的直径,弦CD⊥AB于点E,AE = 1寸,CD = 10寸,求直径AB的长.请你解答这个问题.

-
科目: 来源: 题型:
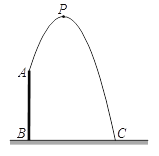
查看答案和解析>>【题目】如图,人工喷泉有一个竖直的喷水枪AB,喷水口A距地面2m,喷出水流的运动路线是抛物线. 如果水流的最高点P到喷水枪AB所在直线的距离为1m,且到地面的距离为3.6m,求水流的落地点C到水枪底部B的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是⊙O的直径,点
是⊙O的直径,点 是
是 的中点,连接
的中点,连接 并延长至点
并延长至点 ,使
,使 ,点
,点 是
是 上一点,且
上一点,且 ,
,  的延长线交
的延长线交 的延长线于点
的延长线于点 ,
,  交⊙O于点
交⊙O于点 ,连接
,连接 .
.(1)求证:
 是⊙O的切线;
是⊙O的切线;(2)当
 时,求
时,求 的长.
的长.
-
科目: 来源: 题型:
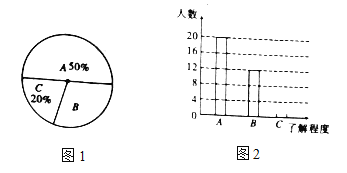
查看答案和解析>>【题目】为传播奥运知识,小刚就本班学生对奥运知识的了解程度进行了一次调查统计:A:熟悉,B:了解较多,C:一般了解图1和图2是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)求该班共有多少名学生;
(2)在条形图中,将表示“一般了解”的部分补充完整;
(3)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数;
(4)如果全年级共1000名同学,请你估算全年级对奥运知识“了解较多”的学生人数.
相关试题

