【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)求C、D两点坐标及△BCD的面积;
(3)若点P在x轴上方的抛物线上,满足S△PCD=![]() S△BCD,求点P的坐标.
S△BCD,求点P的坐标.

参考答案:
【答案】(1)y=﹣(x﹣1)2+4;(2)C(﹣1,0),D(3,0);6;(3)P(1+![]() ,
,![]() ),或P(1﹣
),或P(1﹣![]() ,
,![]() )
)
【解析】
试题分析:(1)设抛物线顶点式解析式y=a(x﹣1)2+4,然后把点B的坐标代入求出a的值,即可得解
(2)令y=0,解方程得出点C,D坐标,再用三角形面积公式即可得出结论;(3)、先根据面积关系求出点P的坐标,求出点P的纵坐标,代入抛物线解析式即可求出点P的坐标.
试题解析:(1)、∵抛物线的顶点为A(1,4), ∴设抛物线的解析式y=a(x﹣1)2+4,
把点B(0,3)代入得,a+4=3, 解得a=﹣1, ∴抛物线的解析式为y=﹣(x﹣1)2+4;
(2)由(1)知,抛物线的解析式为y=﹣(x﹣1)2+4; 令y=0,则0=﹣(x﹣1)2+4,
∴x=﹣1或x=3, ∴C(﹣1,0),D(3,0); ∴CD=4,∴S△BCD=![]() CD×|yB|=
CD×|yB|=![]() ×4×3=6;
×4×3=6;
(3)由(2)知,S△BCD=![]() CD×|yB|=
CD×|yB|=![]() ×4×3=6;CD=4, ∵S△PCD=
×4×3=6;CD=4, ∵S△PCD=![]() S△BCD,
S△BCD,
∴S△PCD=![]() CD×|yP|=
CD×|yP|=![]() ×4×|yP|=3, ∴|yP|=
×4×|yP|=3, ∴|yP|=![]() , ∵点P在x轴上方的抛物线上,
, ∵点P在x轴上方的抛物线上,
∴yP>0, ∴yP=![]() , ∵抛物线的解析式为y=﹣(x﹣1)2+4; ∴
, ∵抛物线的解析式为y=﹣(x﹣1)2+4; ∴![]() =﹣(x﹣1)2+4,
=﹣(x﹣1)2+4,
∴x=1±![]() , ∴P(1+
, ∴P(1+![]() ,
,![]() ),或P(1﹣
),或P(1﹣![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘轮船以每小时40海里的速度沿正北方向航行,在A处测得灯塔C在北偏西30°方向上,轮船航行2小时后到达B处,在B处测得灯塔C在北偏西60°方向上.当轮船到达灯塔C的正东方向D处时,又航行了多少海里?
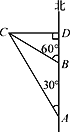
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列6种说法:①∠1与∠4是内错角;②∠1与∠2是同位角;③∠2与∠4是内错角;④∠4与∠5是同旁内角;⑤∠2与∠4是同位角;⑥∠2与∠5是内错角.其中正确的有 ( )

A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天)
1≤x<50
50≤x≤90
售价(元/件)
x+40
90
每天销量(件)
200﹣2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,BF、DE相交于点A,BG交BF于点B,交AC于点C.
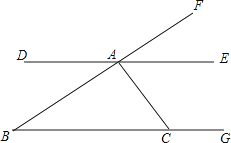
(1)指出ED、BC被BF所截的同位角,内错角,同旁内角;
(2)指出ED、BC被AC所截的内错角,同旁内角;
(3)指出FB、BC被AC所截的内错角,同旁内角. -
科目: 来源: 题型:
查看答案和解析>>【题目】图中的∠1与∠C、∠2与∠B、∠3与∠C,各是哪两条直线被哪一条直线所截形成的同位角?
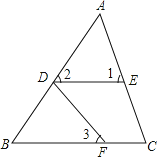
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AD与AE相交于点A,直线BC分别交AD、AE于点B、C,直线DE分别交AD、AE于点D、E,分别写出图中的两对同位角、两对内错角、两对同旁内角.

相关试题

