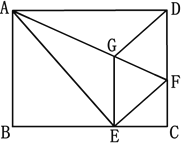
【题目】如图,将矩形ABCD沿线段AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:△AGE≌△AGD
(2)探究线段EG、GF、AF之间的数量关系,并说明理由;
(3)若AG=6,EG=2![]() ,求BE的长.
,求BE的长.
参考答案:
【答案】(1)证明见解析;
(2)AF·GF=2EG![]() ,证明见解析;
,证明见解析;
(3)BE的长为![]() .
.
【解析】(1)证明:∵△AEF是由△ADF折叠得到的
∴AD=AE,∠DAG=∠EAG
又∵AG=AG
∴△AGE≌△AGD
(2)AF×GF=2EG![]() 证明如下:
证明如下:
连接DE交GF于点O

∵△AEF是由△ADF折叠得到的
∠DAG=∠EAG,DF=EF
∵△AGE≌△AGD
∴GD=GE,∠ AGD=∠AGE
∴∠ FGD=∠FGE
∵EG∥CD
∴∠DFG=∠FGE
∴∠ FGD=∠DFG
∴GD=DF
∴GD=EG=EF=DF
∴四边形DGEF是菱形
AF⊥DE,OF=![]() GF
GF
∴∠ADF=∠DOF =90°
又∵∠DFO=∠DFA
∴△DFO∽△AFD
∴![]()
∴OF×AF=DF![]()
∵OF=![]() GF, DF=EG
GF, DF=EG
∴![]() GF×AF= EG
GF×AF= EG![]()
即:AF×GF=2EG![]()
(2)过点G作GH⊥CD于H

则四边形CHGE是矩形,
∴CE=GH
设GF=x,则AF=6+x
∵AF×GF=2EG![]() EG=2
EG=2![]()
∴x(6+x)=40
解得:x=4
∴GF=4,
∴ AF=6+4=10
在Rt△AEF中
AE=![]()
∴BC=AD=AE=4![]()
∵GH∥AD
∴△FGH∽△FAD
∴![]()
∴![]()
∴CE=GH=![]()
∴BE=BC-CE=4![]() -
-![]() =
=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2x – y – 5 = 0 , 则10 – 6x + 3y =_______。
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式8x2n﹣4xn的公因式是( )
A. 4xnB. 2xn﹣1C. 4xn﹣1D. 2xn﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简(﹣3x2)2x3的结果是( )
A. ﹣6x5B. ﹣3x5C. 2x5D. 6x5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A的坐标为(-2,0),直线
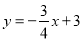 与x轴、y轴分别交于点B和点C,连接AC,顶点为D的抛物线
与x轴、y轴分别交于点B和点C,连接AC,顶点为D的抛物线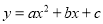 过A、B、C三点.
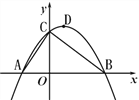
过A、B、C三点.(1)求抛物线的解析式及顶点D的坐标;
(2)设抛物线的对称轴DE交线段BC于点E,P是第一象限内抛物线上一点,过点P作x轴的垂线,交线段BC于点F,若四边形DEFP为平行四边形,求点P的坐标.
(3)设点M是线段BC上的一动点,过点M作MN∥AB,交AC于点N,点Q从点B出发,以每秒1个单位长度的速度沿线段BA向点A运动,运动时间为t(秒),当t(秒)为何值时,存在△QMN为等腰直角三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是一道确定点P位置的尺规作图题的作图过程.
如图,直线L1与L2相交于点O,A,B是L2上两点,点P是直线L1上的点,且∠APB=30°,请在图中作出符合条件的点P.

作法:如图,
(1)以AB为边在L2上方作等边△ABC;
(2)以C 为圆心,AB长为半径作⊙C交直线L1于P1,P2两点.
则P1、P2就是所作出的符合条件的点P.
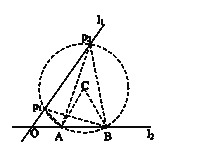
请回答:该作图的依据是______________________________________________________.
-
科目: 来源: 题型:
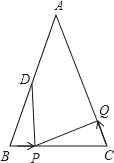
查看答案和解析>>【题目】如图,已知△ABC中,AB=6cm,∠B=∠C,BC=4cm,点D为AB的中点.若点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
相关试题

