【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:

下列结论:
(1)ac<0; (2)当x>1时,y的值随x值的增大而减小.
(3)3是方程ax2+(b-1)x+c=0的一个根;(4)当-1<x<3时,ax2+(b-1)x+c>0.
其中正确的的是_________;(填序号)
参考答案:
【答案】(1)、(3)、(4).
【解析】
试题解析:由图表中数据可得出:x=1时,y=5值最大,所以二次函数y=ax2+bx+c开口向下,a<0;又x=0时,y=3,所以c=3>0,所以ac<0,故(1)正确;
∵二次函数y=ax2+bx+c开口向下,且对称轴为x=![]() =1.5,∴当x>1.5时,y的值随x值的增大而减小,故(2)错误;
=1.5,∴当x>1.5时,y的值随x值的增大而减小,故(2)错误;
∵x=3时,y=3,∴9a+3b+c=3,∵c=3,∴9a+3b+3=3,∴9a+3b=0,
∴9a+3b-3+3=0,
∴3是方程ax2+(b-1)x+c=0的一个根,故(3)正确;
∵x=-1时,ax2+bx+c=-1,∴x=-1时,ax2+(b-1)x+c=0,∵x=3时,ax2+(b-1)x+c=0,且函数有最大值,∴当-1<x<3时,ax2=(b-1)x+c>0,故(4)正确.
故答案为:(1)、(3)、(4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形具有而菱形不具有的性质是( )
A.两组对边分别平行 B.对角线相等
C.对角线互相平分 D.两组对角分别相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据 2,2,4,5,5,8,x,9的平均数为5,则它的众数是( )
A.2
B.4
C.6
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】数据5,5,6,6,6,7,7的众数为_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知函数y=﹣
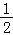 x+3的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M.
x+3的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M.(1)分别求出点A、点M的坐标;
(2)在x轴上有一动点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=﹣
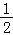 x+3和y=x的图象于点C、D,且OB=2CD,求a的值.
x+3和y=x的图象于点C、D,且OB=2CD,求a的值.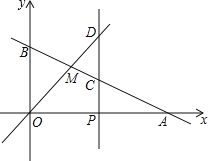
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+mx+(m-1)与x轴交于点A(x1,0),B(x2,0),x1<x2,与y轴交于点C(0,c),且满足x12+x22+x1x2=7.
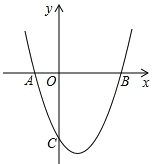
(1)求抛物线的解析式;
(2)在抛物线上能不能找到一点P,使∠POC=∠PCO?若能,请求出点P的坐标;若不能,请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①所有有理数都能用数轴上的点表示; ②符号不同的两个数互为相反数; ③有理数包括整数和分数; ④两数相加,和一定大于任意一个加数.( )
A. 3个 B. 2个 C. 1个 D. 0个
相关试题

