Question

【题目】在Rt△ABC中，∠C=90°，AC=9，BC=12，则点C到AB的距离是（ ）

A． B． C． D．

Answer 1

【答案】A

【解析】

试题分析：根据题意画出相应的图形，如图所示，在直角三角形ABC中，由AC及BC的长，利用勾股定理求出AB的长，然后过C作CD垂直于AB，由直角三角形的面积可以由两直角边乘积的一半来求，也可以由斜边AB乘以斜边上的高CD除以2来求，两者相等，将AC，AB及BC的长代入求出CD的长，即为C到AB的距离．

解：根据题意画出相应的图形，如图所示：

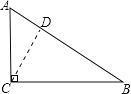
在Rt△ABC中，AC=9，BC=12，

根据勾股定理得：AB==15，

过C作CD⊥AB，交AB于点D，

又S△ABC=ACBC=ABCD，

∴CD===，

则点C到AB的距离是．

故选A