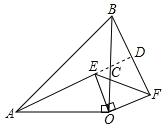
【题目】如图,已知:△OAB,△EOF都是等腰直角三角形,∠AOB=900,中,∠EOF=900,连结AE、BF.
求证:(1) AE=BF;(2) AE⊥BF.

参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)通过证△AEO≌△BFO得到AE=BF;(2)延长AE交BF于D,交OB于C,在△BCD和△ABC中,由∠BCD=∠ACO,∠OAC=∠OBF,可得∠BDA=∠AOB=90°,即可证.
解:(1)在△AEO与△BFO中,
∵Rt△OAB与Rt△EOF是等腰直角三角形,
∴AO=OB,OE=OF,∠AOE=90°-∠BOE=∠BOF,
∴△AEO≌△BFO,
∴AE=BF;
(2)延长AE交BF于D,交OB于C,则∠BCD=∠ACO,
由(1)知△AEO≌△BFO,∴∠OAC=∠OBF,
∴∠BDA=∠AOB=90°,∴AE⊥BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个式子中,是方程的是( )
A.3+2=5
B.x=1
C.2x﹣3<0
D.a2+2ab+b2 -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式
B.平方差公式
C.两数和的完全平方公式
D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在二元一次方程2y+x=8中,若x=0,则y=;若x=2,则y= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(14分) 已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于CE,垂足为H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并说明理由.

-
科目: 来源: 题型:
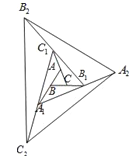
查看答案和解析>>【题目】如图,△ABC的面积为1,分别倍长(延长一倍)AB,BC,CA得到△A1B1C1,再分别倍长A1B1,B1C1,C1A1得到△A2B2C2.…按此规律,倍长n次后得到的△A2017B2017C2017的面积为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明的姐姐在银行工作,她把存入3万元记作+3万元,那么-4万元表示 .
相关试题

