搜索
【题目】①
的解
．
②
的解 ．
③
的解 ．
④
的解 ．…
（1）根据你发现的规律直接写出第⑤，⑥个方程及它们的解．
⑤
⑥
（2）请根据你发现的规律直接写出第
个方程及它的解，并通过计算判断这个结论是否正确．
参考答案：
【答案】（1）
，
；
，
；（2）
，
，计算见解析
【解析】
求出四个方程的解即可；
（1）分别写出第⑤，⑥个方程及它们的解即可；
（2）归纳总结得出一般性规律，写出验证即可．
①
-1的解x=0；
②
-1的解x=1；
③
-1的解x=2；
④
-1的解x=3；
（1）⑤
-1的解x=4；⑥
-1的解x=5；
（2）
-1的解x=n-1，
方程两边同时乘以（x+1），得n=2n-（x+1），
解得x=n-1，
经检验，x=n-1是原方程的解．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知点D、F、E、G都在△ABC的边上，EF∥AD，∠1＝∠2，∠BAC＝70°，求∠AGD的度数．（请在下面的空格处填写理由或数学式）
解：∵EF∥AD，（已知）
∴∠2＝ （ ）
∵∠1＝∠2，（已知）
∴∠1＝ （ ）
∴ ∥ ，（ ）
∴∠AGD+ ＝180°，（两直线平行，同旁内角互补）
∵∠BAC＝70°，（已知）
∴∠AGD＝ （等式性质）
-
科目： 来源： 题型：
查看答案和解析>>【题目】解下列方程： (1)x2-49=0 (2)3x2-7x=0 (3)(2x-1)2=9
(4)x2+3x-4=0 (5)(x+4)2=5(x+4) (6)x2+4x=2
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，Rt△ABC中，∠B=90 ， BC=12，tanC=
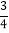． 如果一质点P开始时在AB边的P0处，BP0=3．P第一步从P0跳到AC边的P1（第1次落点）处，且
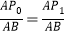；第二步从P1跳到BC边的P2（第2次落点）处，且
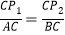；第三步从P2跳到AB边的P3（第3次落点）处，且
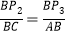；…；质点P按照上述规则一直跳下去，第n次落点为Pn（n为正整数），则点P2014与点P2015之间的距离为（ ）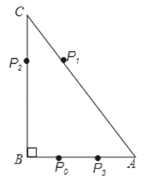
A. 6 B. 5 C. 4 D. 3
-
科目： 来源： 题型：
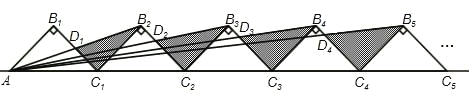
查看答案和解析>>【题目】如图所示，n+1个直角边长为1的等腰直角三角形，斜边在同一直线上，设△B2D1C1的面积为S1，△B3D2C2的面积为S2，…，△Bn+1DnCn的面积为Sn，则S1= ，Sn= （用含n的式子表示）．
-
科目： 来源： 题型：
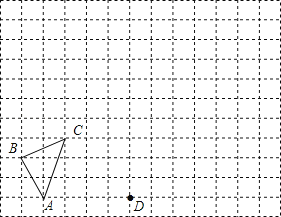
查看答案和解析>>【题目】如图，在由边长为1的单位正方形组成的网格中，按要求画出坐标系及△A1B1C1及△A2B2C2；
（1）若点A、C的坐标分别为（﹣3，0）、（﹣2，3），请画出平面直角坐标系并指出点B的坐标；
（2）画出△ABC关于y轴对称再向上平移1个单位后的图形△A1B1C1；
（3）以图中的点D为位似中心，将△A1B1C1作位似变换且把边长放大到原来的两倍，得到△A2B2C2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，在梯形ABCD中，AB∥CD，∠D=90°，AD=CD=2，点E在边AD上（不与点A、D重合），∠CEB=45°，EB与对角线AC相交于点F，设DE=x．
（1）用含x的代数式表示线段CF的长；
（2）如果把△CAE的周长记作C△CAE，△BAF的周长记作C△BAF，设
=y，求y关于x的函数关系式，并写出它的定义域；（3）当∠ABE的正切值是
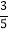时，求AB的长．
相关试题
