【题目】在矩形ABCD中,已知AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,求CE的长.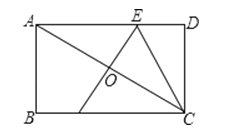
参考答案:
【答案】解:∵四边形ABCD是矩形,
∴AD=BC=4,DC=AB=2,∠D=90°,
∵OE垂直平分AC,
∴EC=AE,
设CE=x,则AE=x,DE=4﹣x,
在△DEC中,由勾股定理得:DE2+DC2=EC2 ,
即(4﹣x)2+22=x2 ,
解得:x=![]() ,
,
∴CE的长是![]() .
.
【解析】由矩形的性质得出AD=BC=4,DC=AB=2,∠D=90°,由线段垂直平分线的性质得出EC=AE,设CE=x,则AE=x,DE=4﹣x,在△DEC中,由勾股定理得出方程,解方程即可.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于同一平面内的直线a、b、c,如果a与b平行,c与a平行,那么c与b的位置关系是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为弘扬中华优秀传统文化,今年2月20日举行了襄阳市首届中小学生经典诵读大赛决赛. 某中学为了选拔优秀学生参加,广泛开展校级“经典诵读”比赛活动,比赛成绩评定为A,B,C,D,E五个等级,该校七(1)班全体学生参加了学校的比赛,并将比赛结果绘制成如下两幅不完整的统计图.请根据图中信息,解答下列问题:
(1)该校七(1)班共有 名学生;扇形统计图中C等级所对应扇形的圆心角等于 度;
(2)补全条形统计图;
(3)若A等级的4名学生中有2名男生2名女生,现从中任意选取2名参加学校培训班,请用列表法或画树状图的方法,求出恰好选到1名男生和1名女生的概率.
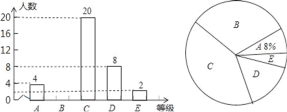
-
科目: 来源: 题型:
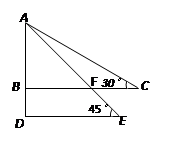
查看答案和解析>>【题目】两个直角三角形如图放置,则∠BFE与∠CAF的度数之比等于( )
A.8
B.9
C.10
D.11 -
科目: 来源: 题型:
查看答案和解析>>【题目】在操场上活动时,小明发现旗杆的影子与旁边的树的影子好像平行,但他不敢确定,那么他可以采取的最好办法是( )
A. 通过平移的办法进行验证
B. 看看其他同学是不是这样认为
C. 构造并测量两个同位角,若相等则影子平行
D. 构造几何模型,用已学知识证明
-
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具专柜要经营一种新上市的儿童玩具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)写出专柜销售这种玩具,每天所得的销售利润W(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该玩具每天的销售利润最大;
(3)专柜结合上述情况,设计了A、B两种营销方案:
方案A:该玩具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件玩具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由.
-
科目: 来源: 题型:
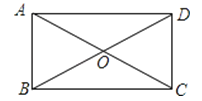
查看答案和解析>>【题目】已知:矩形ABCD中,对角线AC与BD交于点O,∠BOC=120°,AC=4cm,求矩形ABCD的周长.
相关试题

