【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级(1)班学生即将所穿校服型号情况进行摸底调查,并根据调查结果绘制如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).
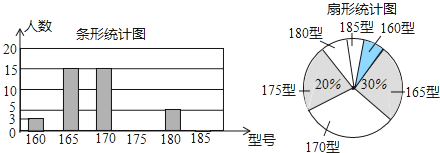
根据以上信息,解答下列问题:
(1)该班共有多少名学生?
(2)在条形统计图中,请把空缺部分补充完整;在扇形统计图中,请计算185型校服所对应的扇形圆心角的大小;
(3)求该班学生所穿校服型号的众数和中位数.如果该高中学校准备招收2000名高一新生,则估计需要准备多少套180型号的校服?
参考答案:
【答案】(1)共有50名学生;(2)答案见解析;14.4°;(3)众数是165和170;中位数是170,200套.
【解析】
(1)利用总人数=165型的人数÷对应的百分比求解即可;
(2)先求出175,185型的学生人数,再补全统计图即可,
(3)利用众数,中位数的定义及2000乘180型号所占的百分比求解即可.
解:(1)15÷30%=50(名),50×20%=10(名),
答:该班共有50名学生,其中穿175型校服的学生有10名;
(2)穿175型校服的学生有10名:50×20%=10(名),
185型的学生人数为:50-3-15-15-10-5=50-48=2(名),
补全统计图如图所示;
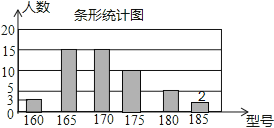
185型校服所对应的扇形圆心角为:![]() ×360°=14.4°;
×360°=14.4°;
(3)165型,170型学生最多,均为15人
∴该班学生所穿校服型号的众数为165,170,
将型号从小到大排列后,第25名和第26名同学均为170型
∴中位数为170.
2000![]() (套)
(套)
∴需要准备200套180型号的校服.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=﹣x+7a+1与直线y=2x﹣2a+4同时经过点P,点Q是以M(0,﹣1)为圆心,MO为半径的圆上的一个动点,则线段PQ的最小值为( )
A.
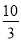 B.
B.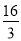 C.
C.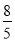 D.
D.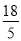
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
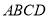 的项点都在坐标轴上,若
的项点都在坐标轴上,若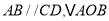 与
与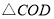 面积分别为
面积分别为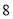 和
和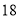 ,若双曲线
,若双曲线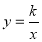 恰好经过
恰好经过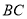 的中点
的中点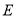 ,则
,则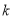 的值为__________.
的值为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
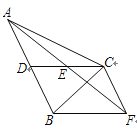
(1) 求证:CF=AD;
(2) 若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三辆汽车经过某收费站下高速时,在2个收费通道A,B中,可随机选择其中的一个通过.
(1)三辆汽车经过此收费站时,都选择A通道通过的概率是 ;
(2)求三辆汽车经过此收费站时,至少有两辆汽车选择B通道通过的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的点A,C在⊙O上,⊙O与AB相交于点D,连接CD,∠A=30°,DC=
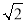 .
.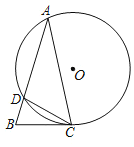
(1)求圆心O到弦DC的距离;
(2)若∠ACB+∠ADC=180°,求证:BC是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量
 (件)与销售单价
(件)与销售单价 (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.
(1)求
 与
与 之间的函数关系式;
之间的函数关系式;(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
相关试题

