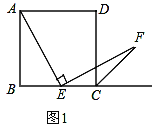
【题目】如图1,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.
(1)求证:AE=EF.
(2)如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点 ”其余条件不变,那么结论AE=EF是否成立呢?若成立,请你证明这一结论,若不成立,请你说明理由.

参考答案:
【答案】(1)证明见解析;(2)成立,证明见解析
【解析】试题分析:(1)取AB的中点G,连接EG,根据已知条件利用ASA判定△AME≌△ECF,因为全等三角形的对应边相等,所以AE=EF.
(2)在AB上取一点M,使AM=EC,连接ME,根据已知条件利用ASA判定△AME≌△ECF,因为全等三角形的对应边相等,所以AE=EF.
试题解析:
(1)证明:取AB的中点G,连接EG
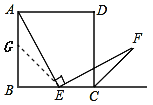
∵四边形ABCD是正方形∴AB=BC,∠B=∠BCD=∠DCG=90°
∵点E是边BC的中点
∴AM=EC=BE
∴∠BGE=∠BEG=45°
∴∠AGE=135°,
∵CF平分∠DCG,
∴∠DCF=∠FCG=45°,
∴∠ECF=180°-∠FCG=135°,
∴∠AGE=∠ECF
∵∠AEF=90°
∴∠AEB+∠CEF=90°,
又∵∠AEB+∠GAE=90°,
∴∠GAE=∠CEF,
在△AGE和△ECF中,∠GAE=∠CEF,AG=CE,∠AGE=∠ECF∴△AGE≌△ECF(ASA),∴AE=EF
(2)证明:在AB上取一点M,使AM=EC,连结ME,
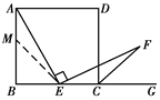
∴BM=BE∴∠BME=45°∴∠AME=135°.
∵CF是外角平分线,
∴∠DCF = 45°.
∴∠ECF = 135°.
∴∠AME = ∠ECF .
∵∠AEB +∠BAE=90°,∠AEB + ∠CEF = 90°,
∴∠BAE = ∠CEF.
∴△AME ≌ △ECF(ASA).
∴AE=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知ax=5,ax+y=30,求ax+ay的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年五一小长假,杭州市公园、景区共接待游客总量617.57万人次,用科学记数法表示617.57万的结果是( )
A. 6.1757×105 B. 6.1757×106 C. 0.61757×106 D. 0.61757×107
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的半径是( )
A. 2.5 cm或6.5 cm
B. 2.5 cm
C. 6.5 cm
D. 5 cm或13cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,PQ切⊙O于T,AC⊥PQ于C,交⊙O于D.
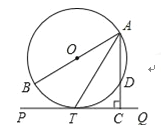
(1)求证:AT平分∠BAC;
(2)若AO=2,AT=
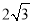 ,求AC的长.
,求AC的长. -
科目: 来源: 题型:
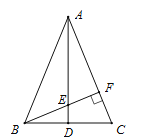
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°
求证:△AEF≌△BCF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】老师和小明同学玩数学游戏.老师取出一个不透明的口袋,口袋中装有三张分别标有数字1,2,3的卡片,卡片除数字外其余都相同,老师要求小明同学两次随机抽取一张卡片,并计算两次抽到卡片上的数字之积是奇数的概率.于是小明同学用画树状图的方法寻求他两次抽取卡片的所有可能结果.如图是小明同学所画的正确树状图的一部分.
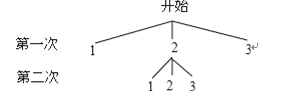
(1)补全小明同学所画的树状图;
(2)求小明同学两次抽到卡片上的数字之积是奇数的概率.
相关试题

