搜索
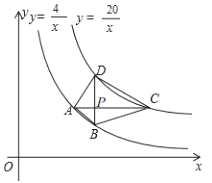
【题目】如图，四边形ABCD的四个顶点分别在反比例函数
与
的图象上，对角线
轴，且
于点P．已知点B的横坐标为4．
（1）若点P的纵坐标为2，求直线AB的函数表达式．
（2）若点P是BD的中点，试判断四边形ABCD的形状，并说明理由．
【答案】（1）
；（2）四边形
是菱形，理由见解析
【解析】
（1）利用题意和反比例函数图象求出点A、B的坐标，再利用待定系数法求出直线AB的解析式中k和b的值即可；
（2）关键在于求出点P的坐标，再根据PA＝PC，PB＝PD，BD⊥AC，得出四边形ABCD为菱形．
（1）如图，
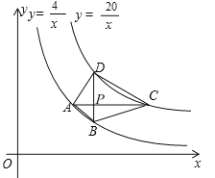
当
时，
，
，
当
时，
，
，
，
设直线
的解析式为
，（k≠0）
，
，
直线的解析式为；
（2）四边形是菱形，
理由如下：如图，
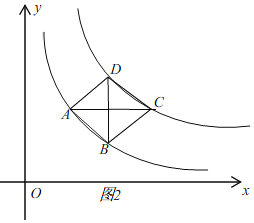
由（1）知，
，
∵BD∥y轴
，
∵点
是线段
的中点，
，
当
时，由
得，
，由
得，
，
，
，
，
又∵PB=PD
四边形为平行四边形，
∵BD⊥AC
四边形是菱形；
