【题目】如图,边长为2的正方形ABCD,点P在边BC上(不与B,C重合),将△ABP沿AP向右翻折,得到△AEP,DE所在直线与AP所在直线交于点F.
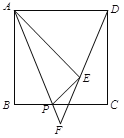
(1)如图,若∠BAP=30°,求∠AFE的度数;
(2)若点E恰为线段DF的中点时,请通过运算说明点P会在线段BC的什么位置?直接写出此时
∠AFD的度数;
(3)若点P是线段BC上任意一点时(不与B,C重合),∠AFD的度数是否会发生变化?试证明你的结论.
参考答案:
【答案】(1)45°;(2)点P在线段BE的垂直平分线上,45°;
(3)∠AFD的度数不会发生变化,理由见解析
【解析】分析:(1)当点P在线段BC上时,由折叠得到一对角相等,再利用正方形性质求出∠DAE度数,在三角形AFD中,利用内角和定理求出所求角度数即可;(2)由E为DF相等,得到P为BC中点,如图1,连接BE交AF于点O,作EG∥AD,得EG∥BC,得到AF垂直平分BE,进而得到三角形BOP与三角形EOG全等,利用全等三角形对应边相等得到BP=EG=1,得到P为BC中点,进而求出所求角度数即可;(3)若点P是线段BC上任意一点时(不与B,C重合),∠AFD的度数不会发生变化,理由为:作AG⊥DF于点G,如图1(a)所示,利用折叠的性质及三线合一性质,根据等式的性质求出∠1+∠2的度数,即为∠FAG度数,即可求出∠F度数;
本题解析:
(1)∵∠EAP=∠BAP=30°,
∴![]() ,
,
在△ADE中,AD=AE,∠DAE=30°,
∴![]() ,
,
在△AFD中,∠FAD=30°+30°=60°,∠ADF=75°,
∴![]() ;
;
(2)点E为DF的中点时,P也为BC的中点,理由如下:
如图1,连接BE交AF于点O,作EG∥AD,得EG∥BC,
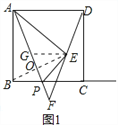
∵EG∥AD,DE=EF,
∴![]() ,
,
∵AB=AE,
∴点A在线段BE的垂直平分线上,
同理可得点P在线段BE的垂直平分线上,
∴AF垂直平分线段BE,
∴OB=OE,
∵GE∥BP,
∴∠OBP=∠OEG,∠OPB=∠OGE,
∴△BOP≌△EOG,
∴BP=EG=1,即P为BC的中点,
![]() 的度数为
的度数为![]() ;
;
(3)∠AFD的度数不会发生变化,
证明:作AG⊥DF于点G,如图2所示,
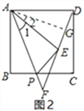
在△ADE中,AD=AE,AG⊥DE,
∵AG平分∠DAE,即∠2=∠DAG,且∠1=∠BAP,
∴![]() ,即∠FAG=45°,
,即∠FAG=45°,
则![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】通过平移得到的新图形中的每一点与原图形中的对应点的连线( )
A.平行
B.相等
C.共线
D.平行(或在同一条直线上)且相等 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,图象一定关于原点对称的图象是( )
A.y=2x
B.y=2x+1
C.y=-2x+1
D.以上三种都不可能有 -
科目: 来源: 题型:
查看答案和解析>>【题目】若某天的最高气温是为6℃,最低气温是﹣3℃,则这天的最高气温比最低气温高________℃.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣2mx以下各点不可能成为二次函数顶点的是( )
A. (﹣2,4) B. (﹣2,﹣4) C. (﹣1,﹣1) D. (1,﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
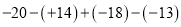 ;
; (2)
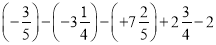
(3)
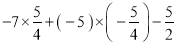 ;
; (4)
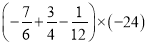
(5)
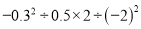
(6)-14-(1-0.5)×
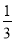 ×[2-(-3)2]
×[2-(-3)2] -
科目: 来源: 题型:
查看答案和解析>>【题目】如果点P(-3,1),那么点P(-3,1)关于原点的对称点P′的坐标是( )
A.(-3,-1)
B.(-3,1)
C.(3,1)
D.(3,-1)
相关试题

