搜索
【题目】（1）已知n正整数，且
，求
的值；
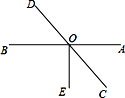
（2）如图，AB、CD交于点O，∠AOE＝90°，若∠AOC︰∠COE＝5︰4，求∠AOD的度数．
参考答案：
【答案】（1）56；（2）130°
【解析】试题分析：（1）先利用积的乘方计算，再利用积的逆运算化成含有a2n的形式，再把a2n=2代入计算即可；（2）由于∠AOC与∠EOC互余，∠AOC：∠COE=5：4，所以∠AOC的度数可求，再根据邻补角的定义求解即可．
试题解析：（1）原式=9a6n-4a4n=9（a2n）3-4（a2n）2
当a2n=2时，原式=9×23-16=56．
（2）∵∠AOE=90°，
∴∠AOC+∠EOC=90°，
∵∠AOC:∠COE=5:4，
∴∠AOC=90°×
=50°，
∴∠AOD=180°50°=130°.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知直线
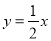与双曲线y＝
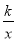交于A、B两点，点B的坐标为(-4，-2)，C为第一象限内双曲线y＝
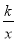上一点，且点C在直线
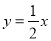的上方．
(1)求双曲线的函数解析式；
(2)若△AOC的面积为6，求点C的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：∠MON＝80°，OE平分∠MON，点A、B、C分别是射线OM、OE、ON上的动点（A、B、C不与点O重合），连接AC交射线OE于点D．设∠OAC＝α．
（1）如图1，若AB∥ON，则：
①∠ABO的度数是 ；
②如图2，当∠BAD＝∠ABD时，试求α的值（要说明理由）；
（2）如图3，若AB⊥OM，则是否存在这样的x的值，使得△ADB中有两个相等的角？若存在，直接写出α的值；若不存在，说明理由．（自己画图）
-
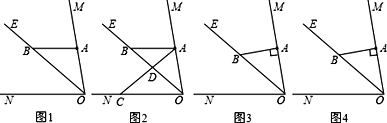
科目： 来源： 题型：
查看答案和解析>>【题目】把分别标有数字2，3，4，5的四个小球放入A袋，把分别标有数字
， 
， 
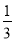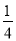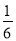的三个小球放入B袋，所有小球的形状、大小、质地均相同，A、B两个袋子不透明．（1）如果从A袋中摸出的小球上的数字为3，再从B袋中摸出一个小球，两个小球上的数字互为倒数的概率是 ；
（2）小明分别从A，B两个袋子中各摸出一个小球，请用树状图或列表法列出所有可能出现的结果，并求这两个小球上的数字互为倒数的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】图1中的摩天轮可抽象成一个圆，圆上一点离地面的高度y（m）与旋转时间x（min）之间的关系如图2所示，根据图中的信息，回答问题：
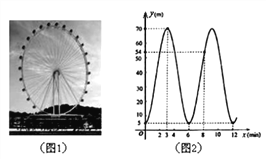
（1）根据图2补全表格：
（2）如表反映的两个变量中，自变量是 ，因变量是 ；
（3）根据图象，摩天轮的直径为 m，它旋转一周需要的时间为 min．
-
科目： 来源： 题型：
查看答案和解析>>【题目】根据下列条件可列出一元一次方程的是( )
A. a与1的和的3倍
B. 甲数的2倍与乙数的3倍的和
C. a与b的差的20%
D. 一个数的3倍是5
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个不透明的袋中装有红、白、黄3种颜色的若干个小球，它们除颜色外完全相同．每次从袋中摸出1个球，记下颜色后放回搅匀再摸．摸球实验中，统计得到下表中的数据：
摸球次数
10
20
50
100
150
200
250
300
400
500
出现红球的频数
4
9
16
31
44
61
74
92
118
147
出现白球的频数
1
4
16
36
52
61
75
85
123
151
由此可以估计摸到黄球的概率约为________（精确到0.1）．
相关试题
