【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件.已知生产一件A种产品,需用甲种原料9千克、乙种原料3千克,可获利润700元;生产一件B种产品,需用甲种原料4千克、乙种原料10千克,可获利润1200元.设生产A种产品的生产件数为x,A、B两种产品所获总利润为y(元).
(1)试写出y与x之间的函数关系式;
(2)求出自变量x的取值范围;
(3)利用函数的性质说明哪种生产方案获总利润最大?最大利润是多少?
参考答案:
【答案】
(1)解:设生产A种产品x件,则生产B种产品(50﹣x)件,
由题意得:y=700x+1200(50﹣x)=﹣500x+60000,
即y与x之间的函数关系式为y=﹣500x+60000
(2)解:由题意得 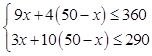 ,
,
解得30≤x≤32.
∵x为整数,
∴整数x=30,31或32
(3)解:∵y=﹣500x+60000,﹣500<0,
∴y随x的增大而减小,
∵x=30,31或32,
∴当x=30时,y有最大值为﹣500×30+60000=45000.
即生产A种产品30件,B种产品20件时,总利润最大,最大利润是45000元
【解析】(1)由于用这两种原料生产A、B两种产品共50件,设生产A种产品x件,那么生产B种产品(50﹣x)件.由A产品每件获利700元,B产品每件获利1200元,根据总利润=700×A种产品数量+1200×B种产品数量即可得到y与x之间的函数关系式;(2)关系式为:A种产品需要甲种原料数量+B种产品需要甲种原料数量≤360;A种产品需要乙种原料数量+B种产品需要乙种原料数量≤290,把相关数值代入得到不等式组,解不等式组即可得到自变量x的取值范围;(3)根据(1)中所求的y与x之间的函数关系式,利用一次函数的增减性和(2)得到的取值范围即可求得最大利润.
【考点精析】掌握一元一次不等式组的应用是解答本题的根本,需要知道1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的两边长分别为2厘米和9厘米,若第三边的长为奇数,则第三边的长为___________厘米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲型H1N1流感病毒的直径大约是0.000000081米,用科学记数法可表示为( )
A. 8.1×10﹣9米B. 8.1×10﹣8米C. 81×10﹣9米D. 0.81×10﹣7米
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知(a+b)2=60,(a-b)2=80,求a2+b2及ab的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按
 元销售时,每天可销售
元销售时,每天可销售 个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出 个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为 元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润 元?
元? -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场服装部为了解服装的销售情况,统计了每位营业员在某月的销售额(单位:万元),并根据统计的这组数据,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题.
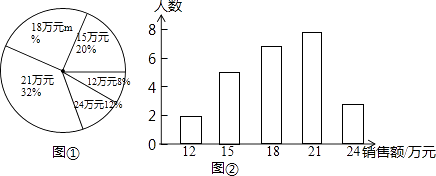
(1)该商场服装部营业员的人数为 , 图①中m的值为
(2)求统计的这组销售额额数据的平均数、众数和中位数. -
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的三边长分别为3、7、a,且a为偶数,则这个三角形的周长为 .
相关试题

