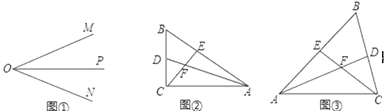
【题目】(1)如图①,OP是∠MON的平分线,点A为OM上一点,点B为OP上一点.请你利用该图形在ON上找一点C,使△COB≌△AOB,请在图①画出图形.参考这个作全等三角形的方法,解答下列问题:
(2)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你写出FE与FD之间的数量关系,并说明理由;
(3)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,在(2)中所得结论是否仍然成立?请你直接作出判断,不必说明理由.
参考答案:
【答案】(1)画图见解析;(2)DF=EF,理由见解析;(3)DF=EF 仍然成立,理由见解析.
【解析】(1)在∠MON的两边上以O为端点截取相等的两条相等的线段,两个端点与角平分线上任意一点相连,所构成的两个三角形全等,即△COB≌△AOB;
(2)根据图(1)的作法,在CG上截取CG=CD,证得△CFG≌△CFD(SAS),得出DF=GF;再根据ASA证明△AFG≌△AFE,得EF=FG,故得出EF=FD;
(3)根据图(1)的作法,在CG上截取AG=AE,证得△EAF≌△GAF(SAS),得出FE=FG;再根据ASA证明△FDC≌△FGC,得DF=FG,故得出EF=FD.
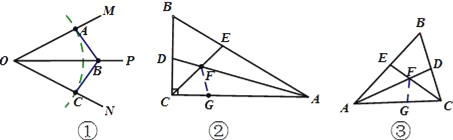
解:(1)如图①所示,△COB≌△AOB,点C即为所求.
(2)如图②,在CG上截取CG=CD,
∵CE是∠BCA的平分线,
∴∠DCF=∠GCF,
在△CFG和△CFD中,
CG=CD,∠DCF=∠GCF,CF=CF,
∴△CFG≌△CFD(SAS),
∴DF=GF.
∵∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,
∴∠FAC=![]() ∠BAC,∠FCA=
∠BAC,∠FCA=![]() ∠ACB,且∠EAF=∠GAF,
∠ACB,且∠EAF=∠GAF,
∴∠FAC+∠FCA=![]() (∠BAC+∠ACB)=
(∠BAC+∠ACB)=![]() =60°,
=60°,
∴∠AFC=120°,
∴∠CFD=60°=∠CFG,
∴∠AFG=60°,
又∵∠AFE=∠CFD=60°,
∴∠AFE=∠AFG,
在△AFG和△AFE中,
∠AFE=∠AFG,AF=AF,∠EAF=∠GAF,
∴△AFG≌△AFE(ASA),
∴EF=GF,
∴DF=EF;
(3)DF=EF 仍然成立.
证明:如图③,在CG上截取AG=AE,
同(2)可得△EAF≌△GAF(SAS),
∴FE=FG,∠EFA=∠GFA.
又由题可知,∠FAC=![]() ∠BAC,∠FCA=
∠BAC,∠FCA=![]() ∠ACB,
∠ACB,
∴∠FAC+∠FCA=![]() (∠BAC+∠ACB)=60°,
(∠BAC+∠ACB)=60°,
∴∠AFC=180°﹣(∠FAC+∠FCA)=120°,
∴∠EFA=∠GFA=180°﹣120°=60°=∠DFC,
∴∠CFG=∠CFD=60°,
同(2)可得△FDC≌△FGC(ASA),
∴FD=FG,
∴FE=FD.
“点睛”此题主要考查全等三角形的判定和性质的运用,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具,在判定三角形全等时,关键是选择恰当的判定条件,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造全等三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=ax+b(a>0)与x轴的交点坐标为(m , 0),则一元一次不等式ax+b≤0的解集应为( )
A.x≤m
B.x≤-m
C.x≥m
D.x≥-m -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个三角形的两条边长分别是1cm和2cm,一个内角为40度.
(1)请你借助图1画出一个满足题设条件的三角形;
(2)你是否还能画出既满足题设条件,又与(1)中所画的三角形不全等的三角形?若能,请你在图1的右边用“尺规作图”作出所有这样的三角形;若不能,请说明理由;
(3)如果将题设条件改为“三角形的两条边长分别是3cm和4cm,一个内角为40°”,那么满足这一条件,且彼此不全等的三角形共有几个.
友情提醒:请在你画的图中标出已知角的度数和已知边的长度,“尺规作图”不要求写作法,但要保留作图痕迹.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是假命题的是( )
A.同旁内角互补
B.对顶角相等
C.直角的补角仍然是直角
D.两点之间,线段最短 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如下图所示.
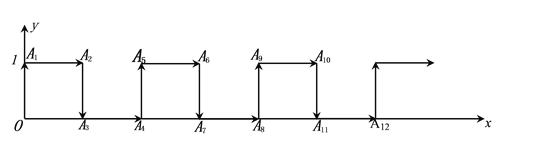
(1)填写下列各点的坐标:A4( , ),A8( , );
(2)点A4n-1的坐标(n是正整数)为( , );
(3)指出蚂蚁从点A2015到点A2016的移动方向.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣4与y轴的交点坐标是( )
A.(0,﹣4)
B.(﹣4,0)
C.(2,0)
D.(0,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形两条边长分别为12、15,则这个三角形的周长为( )
A.27B.39C.42D.39或42
相关试题

