【题目】在学习解直角三角形以后,重庆八中数学兴趣小组测量了旗杆的高度.如图,某一时刻,旗杆AB的影子一部分落在平台上的影长BC为6米,落在斜坡上的影长CD为4米,AB⊥BC,同一时刻,光线与旗杆的夹角为37°,斜坡的坡角为30°,旗杆的高度AB约为( )米.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75, ![]() ≈1.73)
≈1.73)
A.10.61
B.10.52
C.9.87
D.9.37
参考答案:
【答案】A
【解析】解:如图,过点C作CG⊥EF于点G,延长GH交AD于点H,过点H作HP⊥AB于点P,

则四边形BCHP为矩形,
∴BC=PH=6,BP=CH,∠CHD=∠A=37°,
∴AP= ![]() =
= ![]() =8,
=8,
过点D作DQ⊥GH于点Q,
∴∠CDQ=∠CEG=30°,
∴CQ= ![]() CD=2,DQ=CDcos∠CDQ=4×
CD=2,DQ=CDcos∠CDQ=4× ![]() =2
=2 ![]() ,
,
∵QH= ![]() =
= ![]() =
= ![]() ,
,
∴CH=QH﹣CQ= ![]() ﹣2,
﹣2,
则AB=AP+PB=AP+CH=8+ ![]() ﹣2≈10.61,
﹣2≈10.61,
所以答案是:A.
【考点精析】解答此题的关键在于理解解直角三角形的相关知识,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD顶点A、B在x轴上,点D在y轴上,函数y=
 (x>0)的图象经过点C(2,3),直线AD交双曲线于点E,并且EB⊥x轴,CD⊥y轴,EB与CD交于点F.
(x>0)的图象经过点C(2,3),直线AD交双曲线于点E,并且EB⊥x轴,CD⊥y轴,EB与CD交于点F.
(1)若EB= OD,求点E的坐标;
OD,求点E的坐标;
(2)若四边形ABCD为平行四边形,求过A、D两点的函数关系式. -
科目: 来源: 题型:
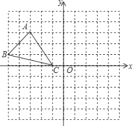
查看答案和解析>>【题目】已知△ABC在平面直角坐标系中的位置如图所示:
(1)画出△ABC关于y轴对称的△A B1C1;并写出B点的对应点B1的坐标;
(2)在y轴上找一点P,使得△PBC的周长最短;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图一,∠ACB=90°,点D在AC上,DE⊥AB垂足为E,交BC的延长线于F,DE=EB,EG=EB,

(1)求证:AG=DF;
(2)过点G作GH⊥AD,垂足为H,与DE的延长线交于点M,如图二,找出图中与AB相等的线段,并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD与AB,CD交于A,D两点,EC,BF与AB,CD交于E,C,B,F,且∠1=∠2,∠B=∠C,

(1)说明CE∥BF.
(2)你能得出∠B=∠3和∠A=∠D这两个结论吗?若能,写出你得出结论的过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,由下列条件可判定哪两条直线平行,并说明根据.

(1)∠1=∠2,________________________.
(2)∠A=∠3,________________________.
(3)∠ABC+∠C=180°,________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知网格上最小的正方形的边长为1.
(1)分别写出A,B,C三点的坐标;
(2)作△ABC关于y轴的对称图形△A′B′C′(不写作法),想一想:关于y轴对称的两个点之间有什么关系?
(3)求△ABC的面积.
相关试题

