【题目】为了解2016年初中毕业生毕业后的去向,某县教育局对部分初三学生进行了抽样调查,就初三学生的四种去向(A,读普通高中;B,读职业高中; C,直接进入社会就业; D,其它)进行数据统计,并绘制了两幅不完整的统计图(a)、(b).请根据图中信息解答下列问题: 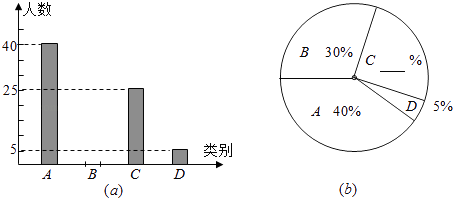
(1)该县共调查了多少名初中毕业生?
(2)通过计算,将两幅统计图中不完整的部分补充完整;
(3)若该县2016年初三毕业生共有4500人,请估计该县今年的初三毕业生中准备读普通高中的学生人数.
参考答案:
【答案】
(1)解:40÷40%=100名,
则该县共调查了100名初中毕业生
(2)解:B的人数:100×30%=30名,
C所占的百分比为: ![]() ×100%=25%,
×100%=25%,
补全统计图如图;
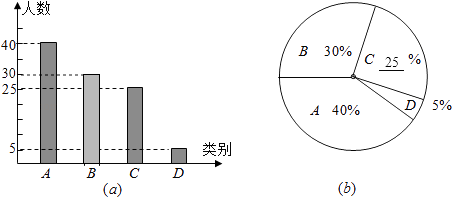
(3)解:根据题意得:4500×40%=1800名,
答:今年的初三毕业生中准备读普通高中的学生人数是1800
【解析】(1)根据A的人数与所占的百分比列式进行计算即可得解;(2)求出B的人数,再求出C所占的百分比,然后补全统计图即可;(3)用总人数乘以A所占的百分比40%,计算即可得解.
【考点精析】关于本题考查的扇形统计图和条形统计图,需要了解能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有A、B、C、D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数分别为﹣5和6,且AC的中点为E,BD的中点为M,BC之间距点B的距离为
 BC的点N,则该数轴的原点为( )
BC的点N,则该数轴的原点为( )
A. 点E B. 点F C. 点M D. 点N
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=5,BC=3,点E为射线BC上一动点,将△ABE沿AE折叠,得到△AB′E.若B′恰好落在射线CD上,则BE的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,
, ,
, 都是正三角形,边长分别为2,
都是正三角形,边长分别为2, ,
, ,
, ,且BO,
,且BO, ,
, ,
, 都在x轴上,点A,
都在x轴上,点A, ,
, ,
, 从左至右依次排列在x轴上方,若点
从左至右依次排列在x轴上方,若点 是BO中点,点
是BO中点,点 是
是 中点,
中点, ,且B为
,且B为 ,则点
,则点 的坐标是
的坐标是


A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①平角就是一条直线;②直线比射线线长;③平面内三条互不重合的直线的公共点个数有0个、1个、2个或3个;④连接两点的线段叫两点之间的距离;⑤两条射线组成的图形叫做角;⑥一条射线把一个角分成两个角,这条射线是这个角的角平分线,其中正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列定义一种关于n的运算:①当n是奇数时,结果为3n+5 ②n为偶数时结果是
 (其中k是使
(其中k是使 是奇数的正整数),并且运算重复进行.例如:取n=26,则…,若n=449,则第449次运算结果是( )
是奇数的正整数),并且运算重复进行.例如:取n=26,则…,若n=449,则第449次运算结果是( )A. 1 B. 2 C. 7 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,有一张长40cm,宽30cm的长方形硬纸片,截去四个小正方形之后,折成如图2所示的无盖纸盒,设无盖纸盒高为xcm.
 用关于x的代数式分别表示无盖纸盒的长和宽.
用关于x的代数式分别表示无盖纸盒的长和宽. 若纸盒的底面积为
若纸盒的底面积为 ,求纸盒的高.
,求纸盒的高. 现根据
现根据 中的纸盒,制作了一个与下底面相同大小的矩形盒盖,并在盒盖上设计了六个总面积为
中的纸盒,制作了一个与下底面相同大小的矩形盒盖,并在盒盖上设计了六个总面积为 的矩形图案
的矩形图案 如图3所示
如图3所示 ,每个图案的高为ycm,A图案的宽为xcm,之后图案的宽度依次递增1cm,各图案的间距、A图案与左边沿的间距、F图案与右边沿的间距均相等,且不小于
,每个图案的高为ycm,A图案的宽为xcm,之后图案的宽度依次递增1cm,各图案的间距、A图案与左边沿的间距、F图案与右边沿的间距均相等,且不小于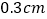 ,求x的取值范围和y的最小值.
,求x的取值范围和y的最小值.
相关试题

