【题目】如图,矩形OABC在平面直角坐标系中,O为坐标原点,点A(0,4),C(2,0).将矩形OABC绕点O按顺时针方向旋转135°,得到矩形EFGH(点E与O重合).
(1)若GH交y轴于点M,则∠FOM=°,OM=;
(2)将矩形EFGH沿y轴向上平移t个单位. ①直线GH与x轴交于点D,若AD∥BO,求t的值;
②若矩形EFGH与矩形OABC重叠部分的面积为S个平方单位,试求当0<t≤4 ![]() ﹣2时,S与t之间的函数关系式.
﹣2时,S与t之间的函数关系式.
参考答案:
【答案】
(1)45;2 ![]()
(2)解:①如图所示:连接AD,BO
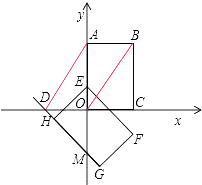
∵AD∥BO,AB∥OD,
∴四边形ADOB为平行四边形,
∴DO=AB=2,
由平移可知:∠HEM=45°,
∴∠OMD=∠ODM=45°,
∴OM=OD=2,
由平移可知:EM=2 ![]() ,
,
∴矩形EFGH平移的路程t=2 ![]() ﹣2=2(
﹣2=2( ![]() ﹣1);
﹣1);
②分三种情况考虑:
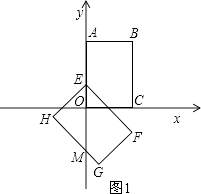
(i)如图1所示,当0<t≤2时,重叠部分为等腰直角三角形,
此时OE=t,则重叠部分面积S= ![]() t2;
t2;
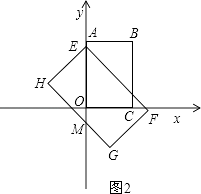
(ii)如图2所示,当2<t≤2 ![]() 时,重叠部分为直角梯形,
时,重叠部分为直角梯形,
此时S= ![]() [(t﹣2)+t]×2=2t﹣2;
[(t﹣2)+t]×2=2t﹣2;
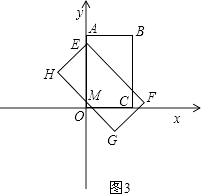
(iii)如图3所示,当2 ![]() <t≤4
<t≤4 ![]() ﹣2时,E点在A点下方,重叠部分为五边形,
﹣2时,E点在A点下方,重叠部分为五边形,
此时S=(2t﹣2)﹣ ![]() (t﹣2
(t﹣2 ![]() )2=﹣
)2=﹣ ![]() t2+2(
t2+2( ![]() +1)t﹣6.
+1)t﹣6.
综上,S= 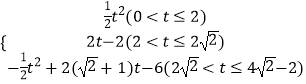 .
.
故答案为:45;2 ![]()
【解析】解:(1)如图所示: 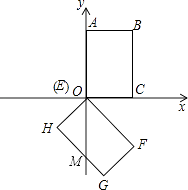
由旋转可得:∠AOF=135°,又∠AOC=90°,
∴∠COF=∠AOF﹣∠AOC=45°,又∠MOC=90°,
∴∠FOM=45°,又OF∥HG,
∴∠OMH=∠FOM=45°,又∠H=90°,
∴△OHM为等腰直角三角形,
∴OH=HM=2,
则根据勾股定理得:OM=2 ![]() ;
;
(1)由旋转可得出∠AOF=135°,再由矩形的内角为直角得到一个角为直角,利用∠AOF﹣∠AOC求出∠COF的度数,再由∠MOC为直角,由∠MOC﹣∠COF即可求出∠MOF的度数;由∠MOF的度数为45°,利用两直线平行得到一对内错角相等,可得出三角形OHM为等腰直角三角形,由OH=MH=2,利用勾股定理即可求出OM的长;(2)①如图所示,当AD与BO平行时,由AB与DO平行,利用两组对边分别平行的四边形为平行四边形得到ABOD为平行四边形,由平行四边形的对边相等得到AB=DO=2,由平移可知:∠HEM=45°,可得出∠OMD=∠ODM=45°,即三角形ODM为等腰直角三角形,得到OD=OM,由OD的长求出OM的长,由三角形HEM为等腰直角三角形,且直角边长为2,利用勾股定理求出EM的长,用EM﹣OM即可求出平移的距离,即为t的值;②分三种情况考虑:(i)如图1所示,当0<t<2时,重叠部分为等腰直角三角形,由平移的距离为t,得到等腰直角三角形直角边为t,利用三角形的面积公式即可表示出S;(ii)如图2所示,当2≤t<2 ![]() 时,重叠部分为直角梯形,表示出上底,下底及高,利用梯形的面积公式表示出S即可;(iii)图3所示,当2
时,重叠部分为直角梯形,表示出上底,下底及高,利用梯形的面积公式表示出S即可;(iii)图3所示,当2 ![]() ≤t≤4
≤t≤4 ![]() ﹣2时,重叠部分为五边形,由梯形面积﹣三角形面积,表示出S即可.
﹣2时,重叠部分为五边形,由梯形面积﹣三角形面积,表示出S即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实施“节能产品惠民工程”一年半以来,国家通过发放补贴的形式支持推广高效节能空调、1.6升及以下排量节能汽车、节能灯三类产品,其中推广节能汽车约120万辆,按每辆3000元标准给予一次性定额补贴.小刚同学根据了解到的信息进行统计分析,绘制出两幅不完整的统计图:

(注:图中A表示“高效节能空调”;B表示“1.6升及以下排量节能汽车”;C表示“节能灯”)
(1)国家对上述三类产品共发放补贴金额亿元,“B”所在扇形的圆心角为°;
(2)补全条形统计图;
(3)国家计划再拿出98亿元继续推广上述三类产品.请你预测,可再推广节能汽车多少万辆? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,点D在AC上,已知∠BDC=45°,BD=10
 ,AB=20.求∠A的度数.
,AB=20.求∠A的度数. 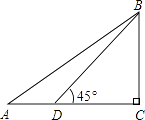
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家和地方政府为了提高农民种粮的积极性,每亩地每年发放种粮补贴120元.种粮大户老王今年种了150亩地,计划明年再承租50~150亩土地种粮以增加收入,考虑各种因素,预计明年每亩种粮成本y(元)与种粮面积x(亩)之间的函数关系如图所示:
(1)今年老王种粮可获得补贴多少元?
(2)根据图象,求y与x之间的函数关系式;
(3)若明年每亩的售粮收入能达到2140元,求老王明年种粮总收入W(元)与种粮面积x(亩)之间的函数关系式.当种粮面积为多少亩时,总收入最高?并求出最高总收入.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解 如图1,△ABC中,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重复部分;…;将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合,无论折叠多少次,只要最后一次恰好重合,∠BAC是△ABC的好角.
小丽展示了确定∠BAC是△ABC的好角的两种情形.情形一:如图2,沿等腰三角形ABC顶角∠BAC的平分线AB1折叠,点B与点C重合;情形二:如图3,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,此时点B1与点C重合.
探究发现
(1)△ABC中,∠B=2∠C,经过两次折叠,∠BAC是不是△ABC的好角?(填“是”或“不是”).
(2)小丽经过三次折叠发现了∠BAC是△ABC的好角,请探究∠B与∠C(不妨设∠B>∠C)之间的等量关系.根据以上内容猜想:若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为 应用提升
(3)小丽找到一个三角形,三个角分别为15°、60°、105°,发现60°和105°的两个角都是此三角形的好角. 请你完成,如果一个三角形的最小角是4°,试求出三角形另外两个角的度数,使该三角形的三个角均是此三角形的好角. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明设计了一个问题,分两步完成:
(1)已知关于x的一元一次方程
 ,请画出数轴,并在数轴上标注a与
,请画出数轴,并在数轴上标注a与 对应的点,分别记作A,B;
对应的点,分别记作A,B;(2)在第1问的条件下,在数轴上另有一点C对应的数为y,C与A的距离是C与B的距离的5倍,且C在表示5的点的左侧,求y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b、c、d都是正实数,且
 <
<  ,给出下列四个不等式: ①
,给出下列四个不等式: ①  <
<  ;②
;②  <
<  ;③
;③  ;④
;④  <
< 
其中不等式正确的是()
A.①③
B.①④
C.②④
D.②③
相关试题

