【题目】试在表格空白处写出下列正多边形的所有对角线条数, 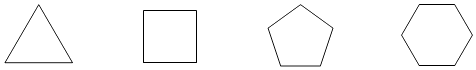
正多边形的边数 | 3 | 4 | 5 | 6 | … |
对角线的条数 | 0 | 2 | … |
根据表,猜想正n边形有条对角线.
参考答案:
【答案】5;9;![]()
【解析】解:从四边形的一个顶点出发可画1条对角线,从五边形的一个顶点出发可画2条对角线,从六边形的一个顶点出发可画3条对角线,请猜想从七边形的一个顶点出发有4条对角线,从n边形的一个顶点出发有(n﹣3)条对角线,从而推导出n边形共有 ![]() 条对角线,
条对角线, ![]() =5(条),
=5(条),![]() =9(条).
=9(条).
填表如下:
正多边形的边数 | 3 | 4 | 5 | 6 | … |
对角线的条数 | 0 | 2 | 5 | 9 | … |
所以答案是:5,9, ![]() .
.
【考点精析】通过灵活运用多边形的对角线,掌握设多边形的边数为n,则多边形的对角线条数为n(n-3)/2即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】单项式﹣3πa3的系数是 , 次数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为______

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分8分) 如图1,某超市从底楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC(精确到0.1米).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)

-
科目: 来源: 题型:
查看答案和解析>>【题目】若3x2﹣2x+b与x2+bx﹣1的和中不存在含x的项,试求b的值,写出它们的和,并证明不论x取什么值,它的值总是正数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式(a-2012)x>a-2012的解集是x<1.则a应满足的条件是( )
A. a=2012 B. a<2012 C. a>2012 D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),C(3,﹣1).
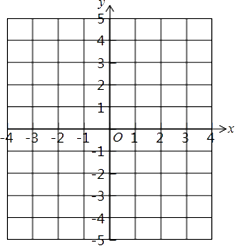
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)求△ABC的面积.
(3)若△A1B1C1与△ABC关于x轴对称,写出A1、B1、C1的坐标,并画出△A1B1C1 .
相关试题

