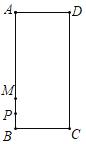
【题目】如图，矩形ABCD中，动点P沿B→A→D→C→B路线运动，点M是AB边上的一点，且MB＝AB，已知AB＝4，BC＝2，AP＝2MP，则点P到边AD的距离为_______．

【答案】2或4

【解析】

根据矩形的性质得到BC＝AD＝2，CD＝AB＝4，求得BM＝1，AM＝3，①当点P在AB边上时，MB＝AB，AB＝4，BC＝2，AP＝2MP，可求出AP即是点P到边AD的距离②当P在CD边上时，如图2，过M作ME⊥CD于E，根据勾股定理得到点P到边AD的距离为4；③P在BC边上时，点P到边AD的距离为4；于是得到结论．

∵四边形ABCD是矩形，AB＝4，BC＝2，

∴BC＝AD＝2，CD＝AB＝4，

∵MB＝AB，

∴BM＝1，AM＝3，

①当点P在AB边上时，

∵AP＝2MP，BM＝1，AM＝3

∴P在线段AM上，

∴AP+PM＝3，

∴AP＝2，

∵AP⊥AD，

∴点P到边AD的距离为2；

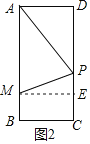
②当P在CD边上时，如图2，

过M作ME⊥CD于E，

则四边形BCEM是矩形，

∴ME＝BC＝2，CE＝BM＝1，

设PD＝x，则PE＝|3﹣x|，

∵PA＝＝，PM＝，

∵PA＝2PM，

∴＝2，

解得：x＝4，

∴点P到边AD的距离为4；

③P在BC边上时，点P到边AD的距离为4；

综上所述，点P到边AD的距离为2或4，

故答案：2或4

关闭