搜索
【题目】已知二次函数y=ax2+bx+c的图象如图所示，对称轴为直线x=1，则下列结论正确的是（ ）
A. ac＞0 B. 当x＞0时，y随x的增大而减小
C. 2a﹣b=0 D. 方程ax2+bx+c=0的两根是x1=﹣1，x2=3
参考答案：
【答案】D
【解析】
根据二次函数图形的开口方向、对称轴的位置、及由坐标轴的交点对选项逐一判断即可.
∵抛物线的开口向下，与y轴的交点在y轴正半轴，
∴a<0，c>0，
∴ac<0，故A选项错误，
∵对称轴是x=1，
∴x>1时y随x的增大而减小，故B选项错误，
∵对称轴为x=-
=1，
∴2a+b=0，故C选项错误，
∵对称轴为x=1，抛物线与x轴的一个交点为（3，0），
∴另一个交点为（-1，0）
∴方程ax2+bx+c=0的两根是x1=﹣1，x2=3，故D选项正确，
故选D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在直角坐标系中，四边形
各个顶点坐标分别为
，
，
．
画出平面直角坐标系，并画四边形．
试确定图中四边形的面积．
如果将四边形绕点
旋转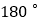
，试确定旋转后四边形上各个顶点的坐标．
如果
，你能重新建立适当的坐标系，横坐标乘以
得的图形与原图形重合吗？请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知
与
是两个大小不同的等腰直角三角形．
如图①所示，连接
，
，试判断线段和的数量和位置关系，并说明理由；
如图②所示，连接，将线段绕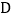
点顺时针旋转
到
，连接
，试判断线段
和的数量和位置关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，AB=BC，将△ABC绕点B顺时针旋转α度，得到△A1BC1，A1B交AC于E，A1C1分别交AC、BC于点D、F，下列结论：①∠CDF=α，②A1E=CF，③DF=FC，④AD=CE，⑤A1F=CE．其中一定正确的有
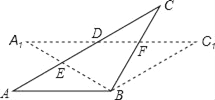
A. ①②④ B. ②③④ C. ①②⑤ D. ③④⑤
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c的顶点M在第二象限，且经过点 A(1，0)和点 B(0，2)．则
（1）a 的取值范围是________；
（2）若△AMO的面积为△ABO面积的
倍时，则a的值为________ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，边长为1的正方形ABCD的对角线AC，BD相交于点O，直角∠MPN的顶点P与点O重合，直角边PM，PN分别与OA，OB重合，然后逆时针旋转∠MPN，旋转角为θ（0°＜θ＜90°），PM、PN分别交AB、BC于E、F两点，连接EF交OB于点G，则下列结论中正确的是_____.
（1）EF=
OE；（2）S四边形OEBF：S正方形ABCD=1：4；（3）在旋转过程中，当△BEF与△COF的面积之和最大时，AE=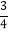
；（4）OGBD=AE2+CF2.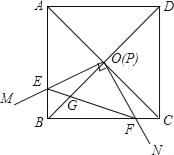
-
科目： 来源： 题型：
查看答案和解析>>【题目】在数学活动课上,老师提出这样一个问题：“已知
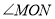，同学们只用一块三角板可以画出它的角平分线吗？”聪明的小阳经过思考设计了如下方案（如图）：（1）在角的两边OM、ON上分别取OA=OB；
（2）过点A作DA⊥OM于点A，交ON于点D；过点B作EB⊥ON于点B，交OM于点E，AD、BE交于点C；
（3）作射线OC.
小阳接着解释说：“此时，△OAC≌△OBC，所以射线OC为∠MON的平分线。”小阳的方案中,△OAC≌△OBC的依据是（ ）
A.SASB.ASAC.HLD.AAS
相关试题
