【题目】已知:如图,在Rt△ABC和Rt△BCD中,∠ABC=∠BCD=90°,BD与AC相交于点E,AB=9,cos∠BAC=![]() ,tan∠DBC=
,tan∠DBC=![]() .
.
求:(1)边CD的长;
(2)△BCE的面积.

参考答案:
【答案】(1)CD=5;(2)![]()
【解析】试题分析:(1)先在Rt△ABC中,由余弦定理求得AC的值,进而理由勾股定理计算出BC,再在Rt△BCD中由正切定理解得CD的长;(2)通过做AB的平行线EH构造出相似三角形,由相似三角形对应边成比例可求得线段EH的长,最后理由三角形面积公式即可求解.
试题解析:(1)在Rt△ABC中, ![]() .
.
∴![]() ,
,
∴BC=![]() .
.
在Rt△BCD中, ![]() ,
,
∴CD=5.
(2)过点E作EH⊥BC,垂足为H,
∵∠ABC=∠BCD=90°,∴∠ABC+∠BCD=180°,∴CD//AB.
∴![]() .
.
∵∠EHC=∠ABC=90°,∴EH//AB,∴ ![]() .
.
∴![]() .
.
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小王在下面的计算中只做对了一道题,他做对的题目是( )
A.3a72a6=6a42
B.(a7)6=a42
C.a42÷a7=a6
D.a6+a6=a12 -
科目: 来源: 题型:
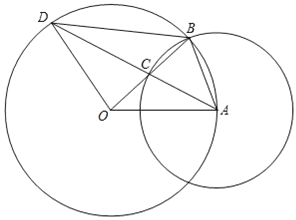
查看答案和解析>>【题目】如图,已知⊙O的半径OA的长为2,点B是⊙O上的动点,以AB为半径的⊙A与线段OB相交于点C,AC的延长线与⊙O相交于点D.设线段AB的长为x,线段OC的长为y.
(1)求y关于x的函数解析式,并写出定义域;
(2)当四边形ABDO是梯形时,求线段OC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”,如图1中四边形ABCD就是一个“格点四边形”.
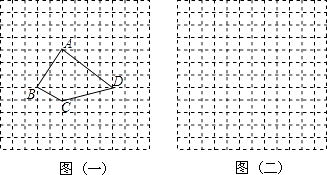
(1)求图1中四边形ABCD的面积;
(2)在图2方格纸中画一个格点三角形EFG,使△EFG的面积等于四边形ABCD的面积且为轴对称图形. -
科目: 来源: 题型:
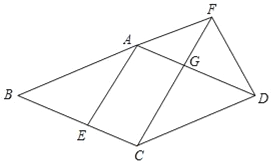
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,点E在边BC上,点F在BA的延长线上,BE=AF,CF∥AE,CF与边AD相交于点G.
求证:(1)FD=CG;
(2)CG2=FGFC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式计算正确的是( )
A.x4x2=x8
B.(x4y3)2=x4y5
C.6x23xy=18x3y
D.a4+a7=a11 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a,b)在第一象限,那么点B(﹣b,﹣a)在( )
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
相关试题

