【题目】襄阳市某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:
![]()
(1)若企业销售该产品获得自睥利润为W(万元),请直接写出年利润W(万元)关于售价(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利澜不少于750万元,试确定该产品的售价x(元/件)的取值范围.
参考答案:
【答案】(1)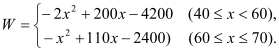 (2)当该产品的售价定为50元/件时,销售该产品的年利润最大,最大利润为800万元.(3)要使企业销售该产品的年利润不少于750万元,该产品的销售价x(元/件)的取值范围为45≤x≤55.
(2)当该产品的售价定为50元/件时,销售该产品的年利润最大,最大利润为800万元.(3)要使企业销售该产品的年利润不少于750万元,该产品的销售价x(元/件)的取值范围为45≤x≤55.
【解析】
试题分析:(1)根据“年利润=年销售量×每件产品的利润(每件产品的售价-每件产品的进价)”直接列出式子,化简即可;(2)根据二次函数的性质,分别计算出两种情况的最大值,比较即可得结论;(3)先由(2)的结论,排除第二种情况,再根据二次函数的性质,由第一种情况确定x的取值范围.
试题解析:(1)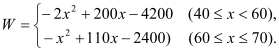
(2)由(1)知,当540≤x<60时,W=-2(x-50)2+800.
∵-2<0,,∴当x=50时。W有最大值800.
当60≤x≤70时,W=-(x-55)2+625.
∵-1<0, ∴当60≤x≤70时,W随x的增大而减小。
∴当x=60时,W有最大值600.
![]()
∴当该产品的售价定为50元/件时,销售该产品的年利润最大,最大利润为800万元.
(3)当40≤x<60时,令W=750,得
-2(x-50)2+800=750,解之,得![]()
由函数W=-2(x-50)2+800的性质可知,
当45≤x≤55时,W≥750.
当60≤x≤70时,W最大值为600<750.
所以,要使企业销售该产品的年利润不少于750万元,该产品的销售价x(元/件)的取值范围为45≤x≤55.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:3ab2+a2b=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
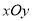 中,对于任意三点
中,对于任意三点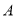 ,
, 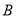 ,
, 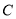 的“矩面积”,给出如下定义:任意两点横坐标差的最大值称为“水平底”
的“矩面积”,给出如下定义:任意两点横坐标差的最大值称为“水平底”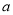 ,任意两点纵坐标差的最大值称为“铅垂高”
,任意两点纵坐标差的最大值称为“铅垂高”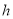 ,“水平底”与“铅垂高”的乘积为点
,“水平底”与“铅垂高”的乘积为点 ,
, 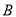 ,
, 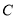 的“矩面积
的“矩面积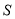 ”,即“矩面积”
”,即“矩面积”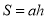 .
.例如:点
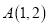 ,
, 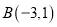 ,
, 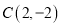 ,它们的“水平底”
,它们的“水平底”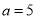 ,“铅垂高”
,“铅垂高”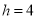 ,“矩面积”
,“矩面积”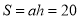 .
. (1)已知点
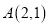 ,
, 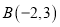 ,
, 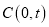 .
. ①若
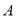 ,
, 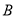 ,
, 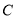 三点的 “矩面积”为12,写出点
三点的 “矩面积”为12,写出点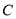 的坐标: ;
的坐标: ;②写出
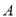 ,
, 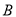 , img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/28/23/79963a76/SYS201712282330522238895478_ST/SYS201712282330522238895478_ST.027.png" width="16" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />三点的“矩面积”的最小值: .
, img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/28/23/79963a76/SYS201712282330522238895478_ST/SYS201712282330522238895478_ST.027.png" width="16" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />三点的“矩面积”的最小值: . (2)已知点
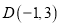 ,
, 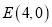 ,
, 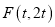 ,
,①当D,E,F三点的“矩面积”取最小值时,写出
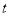 的取值范围: ;
的取值范围: ;②若D,E,F三点的“矩面积”为33,求点
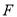 的坐标;
的坐标;③设D,E,F三点的“矩面积”为
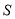 ,写出
,写出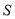 与t的函数关系式.
与t的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】以下四个命题:①一个多边形的内角和为900°,从这个多边形同一个顶点可画的对角线有4条;②三角形的三条高所在的直线的交点可能在三角形的内部或外部;③多边形的所有内角中最多有3个锐角;④△ABC中,若∠A=2∠B=3∠C,则△ABC为直角三角形.其中真命题的是_______________.(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算-7-1的结果为( )
A. 7 B. -6 C. -8 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程ax2﹣4x﹣1=0是一元二次方程,则a满足的条件是( )
A. a>0 B. a≠0 C. a<0 D. a≠4
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算m2+2m2的结果是( )
A. 2m4 B. 3m2 C. 3m4 D. 2m2
相关试题

