【题目】如图,已知正方形ABCD的边长为4,点P是AB边上的一个动点,连接CP,过点P作PC的垂线交AD于点E,以 PE为边作正方形PEFG,顶点G在线段PC上,对角线EG、PF相交于点O. 
(1)若AP=1,则AE=;
(2)①求证:点O一定在△APE的外接圆上; ②当点P从点A运动到点B时,点O也随之运动,求点O经过的路径长;
(3)在点P从点A到点B的运动过程中,△APE的外接圆的圆心也随之运动,求该圆心到AB边的距离的最大值.
参考答案:
【答案】
(1)![]()
(2)①证明:∵PF⊥EG,
∴∠EOF=90°,
∴∠EOF+∠A=180°,
∴A、P、O、E四点共圆,
∴点O一定在△APE的外接圆上;
②解:连接OA、AC,如图1所示:

∵四边形ABCD是正方形,
∴∠B=90°,∠BAC=45°,
∴AC= ![]() =4
=4 ![]() ,
,
∵A、P、O、E四点共圆,
∴∠OAP=∠OEP=45°,
∴点O在AC上,
当P运动到点B时,O为AC的中点,OA= ![]() AC=2
AC=2 ![]() ,
,
即点O经过的路径长为2 ![]() ;
;
(3)解:设△APE的外接圆的圆心为M,作MN⊥AB于N,如图2所示:

则MN∥AE,
∵ME=MP,
∴AN=PN,
∴MN= ![]() AE,
AE,
设AP=x,则BP=4﹣x,
由(1)得:△APE∽△BCP,
∴ ![]() ,即
,即 ![]() ,
,
解得:AE=x﹣ ![]() x2=﹣
x2=﹣ ![]() (x﹣2)2+1,
(x﹣2)2+1,
∴x=2时,AE的最大值为1,此时MN的值最大= ![]() ×1=
×1= ![]() ,
,
即△APE的圆心到AB边的距离的最大值为 ![]() .
.
【解析】(1)解:∵四边形ABCD、四边形PEFG是正方形, ∴∠A=∠B=∠EPG=90°,PF⊥EG,AB=BC=4,∠OEP=45°,
∴∠AEP+∠APE=90°,∠BPC+∠APE=90°,
∴∠AEP=∠PBC,
∴△APE∽△BCP,
∴ ![]() ,即
,即 ![]() ,
,
解得:AE= ![]() ;
;
故答案为: ![]() ;
;
(1)由正方形的性质得出∠A=∠B=∠EPG=90°,PF⊥EG,AB=BC=4,∠OEP=45°,由角的互余关系证出∠AEP=∠PBC,得出△APE∽△BCP,得出对应边成比例即可求出AE的长;(2)①A、P、O、E四点共圆,即可得出结论;②连接OA、AC,由光杆司令求出AC=4 ![]() ,由圆周角定理得出∠OAP=∠OEP=45°,周长点O在AC上,当P运动到点B时,O为AC的中点,即可得出答案;(3)设△APE的外接圆的圆心为M,作MN⊥AB于N,由三角形中位线定理得出MN=
,由圆周角定理得出∠OAP=∠OEP=45°,周长点O在AC上,当P运动到点B时,O为AC的中点,即可得出答案;(3)设△APE的外接圆的圆心为M,作MN⊥AB于N,由三角形中位线定理得出MN= ![]() AE,设AP=x,则BP=4﹣x,由相似三角形的对应边成比例求出AE=x﹣
AE,设AP=x,则BP=4﹣x,由相似三角形的对应边成比例求出AE=x﹣ ![]() x2=﹣
x2=﹣ ![]() (x﹣2)2+1,由二次函数的最大值求出AE的最大值为1,得出MN的最大值=
(x﹣2)2+1,由二次函数的最大值求出AE的最大值为1,得出MN的最大值= ![]() 即可.
即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF.

(1)判断直线DE与半圆O的位置关系,并说明理由;
(2)①求证:CF=OC; ②若半圆O的半径为12,求阴影部分的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定:三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差.如图1,在△ABC中,AO是BC边上的中线,AB与AC的“极化值”就等于AO2﹣BO2的值,可记为AB△AC=AO2﹣BO2 .
(1)在图1中,若∠BAC=90°,AB=8,AC=6,AO是BC边上的中线,则AB△AC= , OC△OA=;
(2)如图2,在△ABC中,AB=AC=4,∠BAC=120°,求AB△AC、BA△BC的值;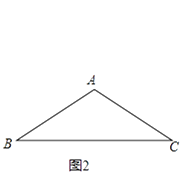
(3)如图3,在△ABC中,AB=AC,AO是BC边上的中线,点N在AO上,且ON= AO.已知AB△AC=14,BN△BA=10,求△ABC的面积.
AO.已知AB△AC=14,BN△BA=10,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克)
30
35
40
45
50
日销售量p(千克)
600
450
300
150
0
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润﹣日支出费用) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,则关于四边形EFGH,下列说法正确的为( )

A.一定不是平行四边形
B.一定不是中心对称图形
C.可能是轴对称图形
D.当AC=BD时它是矩形 -
科目: 来源: 题型:
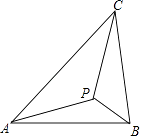
查看答案和解析>>【题目】如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( )
A.5
B.4
C.
D.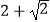
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=
 (x>0)的图象上,顶点B在函数y2=
(x>0)的图象上,顶点B在函数y2=  (x>0)的图象上,∠ABO=30°,则
(x>0)的图象上,∠ABO=30°,则  = .
= . 
相关试题

