【题目】在数学兴趣小组活动中,小明进行数学探究活动.将边长为2的正方形ABCD与边长为3的正方形AEFG按图1位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.
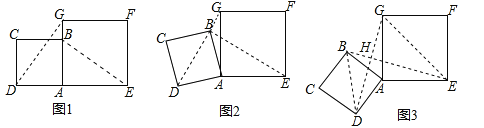
(1)小明发现![]() ,请你帮他说明理由.
,请你帮他说明理由.
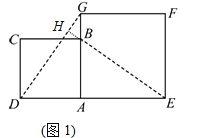
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时△ADG的面积.
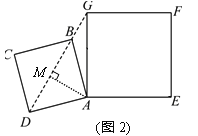
(3)如图3,若小明将正方形ABCD绕点A继续逆时针旋转,顺次连接BD、DE、EG、GB,请你直接写出四边形BDEG面积的最大值 .
参考答案:
【答案】(1)理由见解析;(2)1+![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)利用正方形得到条件,判断出△ADG≌△ABE从而∠AEB+∠ADG=90°,即可;
(2)利用正方形的性质在Rt△AMD中,∠MDA=45°,AD=2从而得出AM=DM=![]() ,在Rt△AMG中,AM2+GM2=AG2从而得出GM=
,在Rt△AMG中,AM2+GM2=AG2从而得出GM=![]() 即可;
即可;
(3)利用旋转,设旋转角为α,在Rt△AIB中,BI=ABsinα,在Rt△AHD中,DH=ADsinα,从而S四边形BDEG用sinα,即可.
试题解析:(1)如图1,延长EB交DG于点H
∵四边形ABCD与四边形AEFG是正方形
∴AD=AB,∠DAG=∠BAE=90°,AG=AE
∴△ADG≌△ABE(SAS)
∴∠AGD=∠AEB
∵△ADG中∠AGD+∠ADG=90°
∴∠AEB+∠ADG=90°
∵△DEH中,∠AEB+∠ADG+∠DHE=180°
∴∠DHE=90°
∴DG⊥BE.
(2)如图2,过点A作AM⊥DG交DG于点M,
∠AMD=∠AMG=90°
∵BD是正方形ABCD的对角
∴∠MDA=45°
在Rt△AMD中,
∵∠MDA=45°,AD=2
∴AM=DM=![]() 在Rt△AMG中,
在Rt△AMG中,
∵AM2+GM2=AG2
∴GM=![]()
∵DG=DM+GM=![]() +
+![]()
∴S△ADG=![]() DGAM=
DGAM=![]() (
(![]() +
+![]() )×
)×![]() =1+
=1+![]()
(3)如图3,
作DH⊥AE交EA的延长线与H,作BI⊥AG,
∵四边形ABCD是边长为2的正方形,
∴AB=AD=2,
设旋转角为α,
∴∠BIG=α,∠HAD=α,
在Rt△AIB中,BI=ABsinα,
在Rt△AHD中,DH=ADsinα,
∵四边形AEFG是边长为3的正方形,
∴AG=AE=3,
∴S/span>四边形BDEG=S△ABG+S△ABD+S△ADE+S△AEG
=S△ABD+S△AEG+S△ABG+S△ADE
=![]() AB×AD+
AB×AD+![]() AG×AE+
AG×AE+![]() ×AG×BI+
×AG×BI+![]() AE×DH
AE×DH
=![]() AB×AD+
AB×AD+![]() AG×AE+
AG×AE+![]() ×AG×ABsinα+
×AG×ABsinα+![]() AE×ADsinα
AE×ADsinα
=![]() ×2×2+
×2×2+![]() ×3×3+
×3×3+![]() ×3×2sinα+
×3×2sinα+![]() ×3×2sinα
×3×2sinα
=![]() +6sinα
+6sinα
当sinα=1时,S四边形BDEG最大,S四边形BDEG最大=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】全球可被人类利用的淡水总量仅占总水量的0.00003,因此珍惜水,保护水是我们每一位公民义不容辞的责任,其中数字0.00003用科学记数法表示为( )
A.3×10﹣4
B.3×10﹣5
C.0.3×10﹣4
D.0.3×10﹣5 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
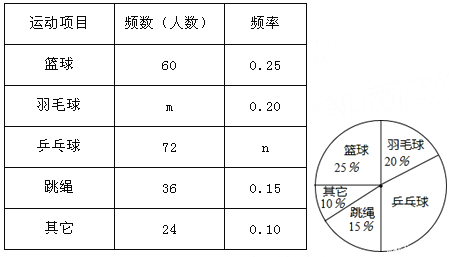
请根据以上图表信息解答下列问题:
(1)频数分布表中的m= ,n= ;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为 °;
(3)从选择“篮球”选项的60名学生中,随机抽取10名学生作为代表进行投篮测试,则其中某位学生被选中的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班围棋兴趣小组的同学在一次活动时,他们用25粒围棋摆成了如图1所示图案,甲、乙、丙3人发现了该图案以下性质:
甲:这是一个中心对称图形;
乙:这是一个轴对称图形,且有4条对称轴;
丙:这是一个轴对称图形,且每条对称轴都经过5粒棋子.
他们想,若去掉其中若干个棋子,上述性质能否仍具有呢?例如,去掉图案正中间一粒棋子(如图2,“×”表示去掉棋子),则甲、乙发现性质仍具有.
请你帮助一起进行探究:

(1)图3中,请去掉4个棋子,使所得图形仅保留甲所发现性质.
(2)图4中,请去掉4个棋子,使所得图形仅保留丙所发现性质.
(3)图5中,请去掉若干个棋子(大于0且小于10),使所得图形仍具有甲、乙、丙3人所发现性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中不正确的是( )
A. 零没有相反数
B. 最大的负整数是﹣1
C. 没有最小的有理数
D. 互为相反数的两个数到原点的距离相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句不是命题的是( )
A. 两直线平行,同位角相等
B. 若|a|=|b|,则a=b
C. 作直线AB垂直于直线CD
D. 同角的补角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠α是锐角,∠α与∠β互补,∠α与∠γ互余,则∠β与∠γ的关系式为( )
A.∠β﹣∠γ=90°
B.∠β+∠γ=90°
C.∠β+∠γ=80°
D.∠β﹣∠γ=180°
相关试题

