【题目】一个问题解决往往经历发现猜想——探索归纳——问题解决的过程,下面结合一道几何题来体验一下.
(发现猜想)(1)如图①,已知∠AOB=70°,∠AOD=100°,OC为∠BOD的角平分线,则∠AOC的度数为 ;.


(探索归纳)(2)如图①,∠AOB=m,∠AOD=n,OC为∠BOD的角平分线. 猜想∠AOC的度数(用含m、n的代数式表示),并说明理由.
(问题解决)(3)如图②,若∠AOB=20°,∠AOC=90°,∠AOD=120°.若射线OB绕点O以每秒20°逆时针旋转,射线OC绕点O以每秒10°顺时针旋转,射线OD绕点O每秒30°顺时针旋转,三条射线同时旋转,当一条射线与直线OA重合时,三条射线同时停止运动. 运动几秒时,其中一条射线是另外两条射线夹角的角平分线?
参考答案:
【答案】(1)85°;(2)∠AOC=![]() ;理由见解析;(3)经过
;理由见解析;(3)经过![]() ,
,![]() ,4秒时,其中一条射线是另外两条射线夹角的平分线.
,4秒时,其中一条射线是另外两条射线夹角的平分线.
【解析】
(1)根据∠AOD、∠AOB、∠BOD之间的关系,求出∠BOD的度数,然后根据角平分线的性质算出∠BOC的度数,再计算∠AOC即可解决问题.
(2)根据∠AOD、∠AOB、∠BOD之间的关系,用m、n表示出∠BOD的度数,然后根据角平分线的性质用m、n的代数式表示出∠BOC,最后再表示出∠AOC即可解决问题.
(3)根据各角之间存在的数量关系,设经过x秒时,分别用x将∠DOA、∠COA、∠BOA表示出来,然后分四类情况讨论,根据角平分线的性质列出方程,解决即可.
(1)85°;
(2)∵∠AOB=m,∠AOD=n
∴∠BOD=n-m
∵OC为∠BOD的角平分线
∴∠BOC=![]()
∴∠AOC=![]() +m=
+m=![]()
(3)设经过的时间为x秒,
则∠DOA=120°-30x;∠COA=90°-10x;∠BOA=20°+20x;
①当在x=![]() 之前,OC为OB,OD的角平分线;30-20x=70-30x,x1=4(舍);
之前,OC为OB,OD的角平分线;30-20x=70-30x,x1=4(舍);
②当x在![]() 和2之间,OD为OC,OB的角平分线;-30+20x=100-50x,x2=
和2之间,OD为OC,OB的角平分线;-30+20x=100-50x,x2=![]() ;
;
③当x在2和![]() 之间,OB为OC,OD的角平分线;70-30x=-100+50x,x3=
之间,OB为OC,OD的角平分线;70-30x=-100+50x,x3=![]() ;
;
④当x在![]() 和4之间,OC为OB,OD的角平分线;-70+30x=-30+20x,x4=4.
和4之间,OC为OB,OD的角平分线;-70+30x=-30+20x,x4=4.
答:经过![]() ,
,![]() ,4秒时,其中一条射线是另外两条射线夹角的平分线.
,4秒时,其中一条射线是另外两条射线夹角的平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四座城市A,B,C,D分别位于一个边长100km的大正方形的四个顶点,由于各城市之间的商业往来日益频繁,于是政府决定修建公路网连接它们,根据实际,公路总长设计得越短越好,公开招标的信息发布后,一个又一个方案被提交上来,经过初审后,拟从下面四个方案中选定一个再进一步认证,其中符合要求的方案是( )




A. B. C. D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下表,回答问题:
x
…
-2
-1
0
1
2
…
-2x+5
…
9
7
5
3
a
…
2x+8
…
4
6
8
10
b
…
(初步感知)
(1)a= ;b= ;
(归纳规律)
(2)随着x值的变化,两个代数式的值变化规律是什么?
(问题解决)
(3)比较-2x+5与2x+8的大小;
(4)请写出一个含x的代数式,要求x的值每增加1,代数式的值减小5,当x=0时,
代数式的值为-7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数分别填入相应的集合里:
﹣|﹣5|, 2.626 626 662…, 0, ﹣π, ﹣
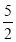 , 0.12, ﹣(﹣6).
, 0.12, ﹣(﹣6).(1)正有理数集合:{ ____________ …};
(2)负数集合:{ ____________ …};
(3)整数集合:{ ____________ …};
(4)分数集合:{ ____________ …}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市预测某饮料会畅销、先用1800元购进一批这种饮料,面市后果然供不应求,又用8100元购进这种饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若两次进饮料都按同一价格销售,两批全部售完后,获利不少于2700元,那么销售单价至少为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(认识概念)
点P、Q分别是两个图形G1、G2上的任意一点,当P、Q两点之间的距离最小时,我们把这个最小距离叫作图形G1、G2的亲密距离,记为d(G1,G2).例如,如果点M、N分别是两条相交直线a、b上的任意一点,则d(a,b)=0
(初步运用)
如图1,长方形四个顶点分别是点A、B、C、D,边AB=CD=5,AD=BC=3.那么d(AB,CD)=___,d(AD,BC)=_____,d(AD,AB)=_____.
(深入探究)
(1)在图1中,如果将线段CD沿它所在直线平移(边AB不动),且使d(CD,AB)不变,那么线段CD的中点偏离它原来位置的最大距离为______;
(2)如图2,线段AB∥直线CD,AB=1,点A到CD的距离为3,将线段AB绕点A旋转90°后的对应线段为AB′,则d(AB′,CD)=______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知忠华家、桂枝家、文兴家及学校在一条南北向的大街旁.一天,放学后他们三人从学校出发,先向南走250米达到桂枝家(记为点A),然后再向南走250米到文兴家(记为点B),从文兴家向北走1000米到达忠华家(记为点C).
(1)以学校为原点,以向北方向为正方向,用1个单位长度表示实际距离250米画出一条数轴,在数轴上用字母表示出忠华家、桂枝家、文兴家的位置.
(2)忠华家在学校的哪个方向,到学校的距离是多少米?
(3)如果以向南方向为正方向建立数轴,对确定忠华家相对于学校的位置有影响吗?说明理由.
相关试题

