【题目】如图.已知某开发区有一块四边形空地ABCD,现计划在该空地上种植草皮,经测量∠ADC=90°,AD=6m,CD=8m,BC=AB=13m,若每平方米草皮需200元,则在该空地上种植草皮共需多少钱?

参考答案:
【答案】在该空地上种植草皮共需7200元
【解析】
在直角三角形ACD中可求得AC的长,过点B作BE⊥AC于点E,利用勾股定理可求出BE的长,进而可求出△ABC的面积,△ADC的面积易求,则四边形空地ABCD的面积可求出,结合已知条件每平方米草皮需200元,则该空地上种植草皮的钱数可求出.
解:过点B作BE⊥AC于点E,
∵∠ADC=90°,AD=6m,CD=8m,
∴AC=![]() =10m,
=10m,
∵BC=AB=13m,
∴AE=CE=![]() AC=5m,
AC=5m,
∴BE=![]() =12m,
=12m,
∴△ABC的面积=![]() ×10×12=60m2,
×10×12=60m2,
∵△ADC的面积=![]() ×6×8=24m2,
×6×8=24m2,
∴边形空地ABCD的面积=60﹣24=36m2,
∴在该空地上种植草皮共需36×200=7200元.

-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算: ÷
÷  ;
;
(2)如图,正方形ABCD中,点E,F,G分别在AB,BC,CD上,且∠EFG=90°.求证:△EBF∽△FCG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一次函数y=﹣
 x+b的图象与y轴交于点B(0,2),与反比例函数y=
x+b的图象与y轴交于点B(0,2),与反比例函数y= 的图象交于点A(4,﹣1).
的图象交于点A(4,﹣1).(1)求反比例函数的表达式和一次函数表达式;
(2)如果点P是x轴上的一点,且△ABP的面积是3,求P点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,是随机事件的是( )
A.任意选择某一电视频道,它正在播放新闻联播
B.三角形任意两边之和大于第三边
C. 是实数,
是实数, 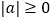
D.在一个装着白球和黑球的袋中摸球,摸出红球 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图的四个转盘中,转盘3,4被分成8等分,若让转盘自由转动一次停止后,指针落在阴影区域内可能性从大到小排列为( )

A.①②④③
B.③②④①
C.③④②①
D.④③②① -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为庆祝国庆节举办游园活动,小军来到摸球兑奖活动场地,李老师对小军说:“这里有甲、乙两个盒子,里面都装有一些乒乓球,你只能选择在其中一个盒子中摸球。”获奖规则如下:
甲盒中有白色乒乓球4个,黄色乒乓球1个,一人只能摸一次且一次摸出一个球,若这个球为黄色球,则可获得玩具熊一个,否则不得奖;
乙盒中有白色乒乓球2个,黄色乒乓球3个,一人只能摸一次且一次摸出两个球,若这两个球均为黄色球,则可获得玩具熊一个,否则不得奖;
请问小军在哪个盒子内摸球获得玩具熊的机会更大?请用概率知识说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,∠B=45°,过点C作CE⊥AD于点,连结AC,过点D作DF⊥AC于点F,交CE于点G,连结EF.
(1)若DG=8,求对角线AC的长;
(2)求证:AF+FG=
 EF.
EF.
相关试题

