【题目】如图,在平面直角坐标系中,Rt△ABO中,∠ABO=90°,OB边在x轴上,将△ABO绕点B顺时针旋转60°得到△CBD.若点A的坐标为(﹣2,2 ![]() ),则点C的坐标为( )
),则点C的坐标为( )
A.( ![]() ,1)
,1)
B.(1, ![]() )
)
C.(1,2)
D.(2,1)
参考答案:
【答案】B
【解析】解:作CH⊥x轴于H,如图,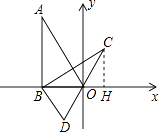
∵点A的坐标为(﹣2,2 ![]() ),AB⊥x轴于点B,∴tan∠BAC=
),AB⊥x轴于点B,∴tan∠BAC= ![]() =
= ![]() ,
,
∴∠A=30°,
∵△ABO绕点B逆时针旋转60°得到△CBD,
∴BC=BA=2 ![]() ,OB=2,∠CBH=30°,
,OB=2,∠CBH=30°,
在Rt△CBH中,CH= ![]() BC=
BC= ![]() ,
,
BH= ![]() CH=3,
CH=3,
OH=BH﹣OB=3﹣2=1,
∴C(1, ![]() ).
).
故选:B.
作CH⊥x轴于H,如图,再利用旋转的性质得BC=BA=2 ![]() ,∠ABC=60°,则∠CBH=30°,然后在Rt△CBH中,利用含30度的直角三角形三边的关系可计算出CH=
,∠ABC=60°,则∠CBH=30°,然后在Rt△CBH中,利用含30度的直角三角形三边的关系可计算出CH= ![]() BC=
BC= ![]() ,BH=
,BH= ![]() CH=3,所以OH=BH﹣OB=3﹣2=1,于是可写出C点坐标.
CH=3,所以OH=BH﹣OB=3﹣2=1,于是可写出C点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现规定一种新运算“※”:a※b=ab,如3※2=32=9,则(﹣2)※3等于_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,DE⊥DF,点E,F分别在AC,BC上,求证:DE=DF.
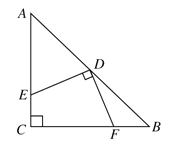
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(π﹣1)
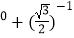 +|5﹣
+|5﹣ 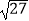 |﹣
|﹣ 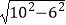 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a3·(-a2)= a5
B.(-ax2)3=-ax6
C.3x3-x(3x2-x+1)=x2-x
D.(x+1)(x-3)=x2+x-3 -
科目: 来源: 题型:
查看答案和解析>>【题目】为传播奥运知识,小刚就本班学生对奥运知识的了解程度进行了一次调查统计:A:熟悉,B:了解较多,C:一般了解.图1和图2是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:

(1)求该班共有多少名学生;
(2)在条形图中,将表示“一般了解”的部分补充完整;
(3)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数;
(4)如果全年级共1000名同学,请你估算全年级对奥运知识“了解较多”的学生人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算2x(3x2+1),正确的结果是( )
A.5x3+2x
B.6x3+1
C.6x3+2x
D.6x2+2x
相关试题

