Question

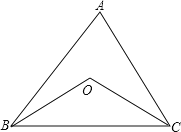
【题目】如图，在等腰△ABC中，∠A=80°，∠B和∠C的平分线相交于点O

（1）连接OA，求∠OAC的度数；

（2）求：∠BOC。

Answer 1

【答案】(1) 40°;(2) 130°

【解析】试题分析：（1）连接AO，利用等腰三角形的对称性即可求得∠OAC的度数；（2）利用三角形的内角和定理以及角平分线的定义求∠BOC与∠A的关系，再把∠A代入即可求∠BOC的度数．

试题解析：

（1）连接AO，

∵在等腰△ABC中，∠B和∠C的平分线相交于点O，

∴等腰△ABC关于线段AO所在的直线对称，

∵∠A=80°，

∴∠OAC=40°

（2）∵BO、CO分别平分∠ABC和∠ACB，

∴∠OBC= ∠ABC，∠OCB=∠ACB，

∴∠BOC=180°-（∠OBC+∠OCB）

=180°-（ ∠ABC+∠ACB）

=180°- （∠ABC+∠ACB）

=180°- （180°-∠A）

=90°+∠A。

∴当∠A=80°时，

∠BOC＝180° (∠B+∠C)＝90°+∠A=130°。