【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表:
x | … | ﹣3 | - | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中m= .
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分;
(3)观察函数图象,写出2条函数的性质;
(4)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所对应的方程x2﹣2|x|=0有
②方程x2﹣2|x|=2有 个实数根.
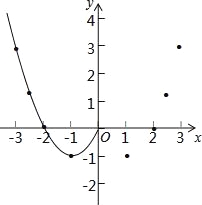
参考答案:
【答案】(1)m=0;(2)答案见解析;(3)答案见解析;(4)3;3;2.
【解析】
试题分析:(1)将x=﹣2代入函数解析式中求出y值,即可得出结论;(2)根据表格数据,描点补充完图形;(3)根据函数图象,寻找出对称轴以及函数的单调区间,此题得解;(4)①观察函数图象,根据函数图象与x轴有3个交点,即可得出结论;②画出直线y=2,观察图形,可得出函数y=x2﹣2|x|的图象与y=2只有2个交点,此题得解.
试题解析:(1)当x=﹣2时,y=(﹣2)2﹣2×|﹣2|=0, ∴m=0,
(2)根据给定的表格中数据描点画出图形,如图1所示.
(3)观察函数图象,可得出:①函数图象关于y轴对称,②当x>1时,y随x的增大而增大.
(4)①观察函数图象可知:当x=﹣2、0、2时,y=0, ∴该函数图象与x轴有3个交点,
即对应的方程x2﹣2|x|=0有3个实数根.
②在图中作直线y=2,如图2所示. 观察函数图象可知:函数y=x2﹣2|x|的图象与y=2只有2个交点.


-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两名运动员,在相同情况下各射击10次.两名的平均数都是8, 方差分别为4.2.2,则成绩较好的是__________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】超市将某品牌的洗涤液按照进价提高50%后标价,再打八折销售,仍可获利30元.则这种商品的进价是_____元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据1,8,3,8,5,3,8的众数是__________是
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.0.720精确到百分位
B.5.078×104精确到千分位
C.36万精确到个位
D.2.90×105精确到千位 -
科目: 来源: 题型:
查看答案和解析>>【题目】﹣5的相反数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.
正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN—∠AMB
=180°—∠B—∠AMB
=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正
 边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)

图1 图2
相关试题

