如图,固定一块三角板,另一块三角板按图示开始平移至两条较大直角边重合时停止.(两个同学为一组,利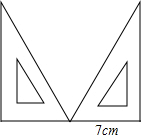 用30°角的三角板作图形的平移运动)
用30°角的三角板作图形的平移运动)
(1)观察平移过程中的重叠部分是什么图形?你能把它画出来吗?
(2)分别求出平移距离为4cm或10cm时,重叠部分的面积.
(3)若平移的距离为x,当x
(4)若重叠部分的面积为Scm3,请写出S关于x的函数关系式.
 用30°角的三角板作图形的平移运动)
用30°角的三角板作图形的平移运动)(1)观察平移过程中的重叠部分是什么图形?你能把它画出来吗?
(2)分别求出平移距离为4cm或10cm时,重叠部分的面积.
(3)若平移的距离为x,当x
≤7cm
≤7cm
时,重叠部分为三角形;当x≥7cm
≥7cm
时,重叠部分为五边形.(4)若重叠部分的面积为Scm3,请写出S关于x的函数关系式.
分析:(1)将右边的一块三角板固定,左边的三角板从左往右平移,观察发现,平移过程中的重叠部分,刚开始的三角形由小到大,后来是五边形;
(2)根据平移距离为4cm或10cm时,重叠部分的图形分别为三角形和五边形,即可求出面积;
(3)由图可知,当x≤7cm时,重叠部分为三角形;当x≥7cm时,重叠部分为五边形;
(4)分两种情况讨论:①当x≤7cm时,重叠部分为三角形;②当14cm≥x≥7cm时,重叠部分为五边形.
(2)根据平移距离为4cm或10cm时,重叠部分的图形分别为三角形和五边形,即可求出面积;
(3)由图可知,当x≤7cm时,重叠部分为三角形;当x≥7cm时,重叠部分为五边形;
(4)分两种情况讨论:①当x≤7cm时,重叠部分为三角形;②当14cm≥x≥7cm时,重叠部分为五边形.
解答:解:(1)平移过程中的重叠部分是三角形或五边形,如下图:
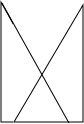
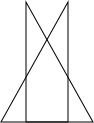
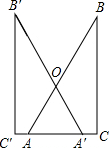
(2)当平移距离为4cm时,重叠部分是三角形OAA′,如右图,此时AA′=4cm.
∵∠OAA′=∠OA′A=60°,
∴△OAA′是等边三角形,
∴S△OAA′=
×42=4
(cm2);
当平移距离为10cm时,重叠部分是五边形ODC′CE,如右图,此时AA′=10cm.
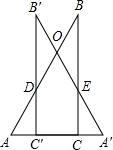 ∵AC=A′C′=7cm,
∵AC=A′C′=7cm,
∴A′C=AC′=3cm,
∵∠A=∠A′=60°,∠AC′D=∠A′CE=90°,
∴C′D=CE=3
cm.
∴S五边形ODC′CE=S△OAA′-S△AC′D-S△A′CE=
×102-
×3×3
×2=25
-9
=16
(cm2);
(3)若平移的距离为x,当x≤7cm时,重叠部分为三角形;当x≥7cm时,重叠部分为五边形;
故答案为≤7cm,≥7cm.

(4)分两种情况讨论:
①当x≤7cm时,重叠部分为三角形OAA′,如右图,此时AA′=x.
∵∠OAA′=∠OA′A=60°,
∴△OAA′是等边三角形,
∴S=S△OAA′=
x2;
 ②当14cm≥x≥7cm时,重叠部分是五边形ODC′CE,如右图,此时AA′=x.
②当14cm≥x≥7cm时,重叠部分是五边形ODC′CE,如右图,此时AA′=x.
∵AC=A′C′=7cm,
∴A′C=AC′=(x-7)cm,
∵∠A=∠A′=60°,∠AC′D=∠A′CE=90°,
∴C′D=CE=
(x-7)cm.
∴S=S五边形ODC′CE=S△OAA′-S△AC′D-S△A′CE=
x2-
×(x-7)×
(x-7)×2=
x2-
(x-7)2=-
x2+14
x-49
.



(2)当平移距离为4cm时,重叠部分是三角形OAA′,如右图,此时AA′=4cm.
∵∠OAA′=∠OA′A=60°,
∴△OAA′是等边三角形,
∴S△OAA′=
| ||
| 4 |
| 3 |
当平移距离为10cm时,重叠部分是五边形ODC′CE,如右图,此时AA′=10cm.
 ∵AC=A′C′=7cm,
∵AC=A′C′=7cm,∴A′C=AC′=3cm,
∵∠A=∠A′=60°,∠AC′D=∠A′CE=90°,
∴C′D=CE=3
| 3 |
∴S五边形ODC′CE=S△OAA′-S△AC′D-S△A′CE=
| ||
| 4 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
(3)若平移的距离为x,当x≤7cm时,重叠部分为三角形;当x≥7cm时,重叠部分为五边形;
故答案为≤7cm,≥7cm.

(4)分两种情况讨论:
①当x≤7cm时,重叠部分为三角形OAA′,如右图,此时AA′=x.
∵∠OAA′=∠OA′A=60°,
∴△OAA′是等边三角形,
∴S=S△OAA′=
| ||
| 4 |
 ②当14cm≥x≥7cm时,重叠部分是五边形ODC′CE,如右图,此时AA′=x.
②当14cm≥x≥7cm时,重叠部分是五边形ODC′CE,如右图,此时AA′=x.∵AC=A′C′=7cm,
∴A′C=AC′=(x-7)cm,
∵∠A=∠A′=60°,∠AC′D=∠A′CE=90°,
∴C′D=CE=
| 3 |
∴S=S五边形ODC′CE=S△OAA′-S△AC′D-S△A′CE=
| ||
| 4 |
| 1 |
| 2 |
| 3 |
| ||
| 4 |
| 3 |
3
| ||
| 4 |
| 3 |
| 3 |
点评:本题考查了平移的性质,等边三角形的判定与性质,解直角三角形,综合性较强,难度中等,得出重叠部分的图形随平移的距离x的变化而变化,进行分类讨论是解题的关键.

