搜索
【题目】如图所示的Rt△ABC中，∠B=90°，点P从点B开始沿BA边以1厘米/秒的速度向点A移动；同时，点Q也从点B开始沿BC边以2厘米/秒的速度向点C移动．问：几秒后△PBQ的面积为35平方厘米？PQ的距离是多少厘米？（结果用最简二次根式表示）
参考答案：
【答案】
秒；5
厘米．
【解析】试题分析：首先设x秒后面积为35，然后得出BP=x，BQ=2x，根据题意列出方程求出x的值，然后根据Rt△BPQ的勾股定理得出距离．
试题解析：设x 后△PBQ的面积为35平方厘米．则有PB=x，BQ=2x
依题意，得： 
x·2x=35 x2=35 解得：x=
∴
秒后△PBQ的面积为35平方厘米．
PQ=
=5
答： 
秒后△PBQ的面积为35平方厘米，PQ的距离为5
厘米．
-
科目： 来源： 题型：
查看答案和解析>>【题目】不等式3（x﹣1）≤5﹣x的非负整数解有（ ）
A.1个
B.2个
C.3个
D.4个 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，AD=5，AB=8，点E是DC上一点，将∠D沿折痕AE折叠，使点D落在点D′处，当△AD′B为等腰三角形时，则DE的长为______________．
-
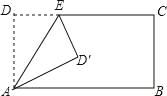
科目： 来源： 题型：
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a元收费,超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按b元收费,该市小明家今年9、10月份的用水量和所交水费如下表所示:
月份
用水量(m3)
收费(元)
9
5
7.5
10
9
18
设小明家每月用水量x(立方米),应交水费y(元).
⑴则a= ,b= ；
⑵ 当x≤6,x＞6时,分别写出y与x的函数关系式；
⑶ 若该户11月份、12月份用水量为14立方米共交水费27元（11月份用水小于12月份用水）,求该户11月份水、12月份用水各多少立方米?
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商品原价100元，连续两次涨价后，售价为144元．若平均增长率为x，则x= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某县地震牵动着全国人民的心，某单位开展了“一方有难，八主支援”赈灾捐款活动．第一天收到捐款10000元，第三天收到捐款12100元，如果第二天、第三天、第四天的平均增长率相同，则第四天收到的捐款为（ ）
A. 13150元 B. 13310元 C. 13400元 D. 14200元
-
科目： 来源： 题型：
查看答案和解析>>【题目】因式分解：a2+ab= ．
相关试题
