【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点A和B.
轴分别相交于点A和B.
(1)直接写出坐标:点A ,点B ;
(2)以线段AB为一边在第一象限内作□ABCD,其顶点D(![]() ,
, ![]() )在双曲线
)在双曲线![]() (
(![]() >
>![]() )上.
)上.
①求证:四边形ABCD是正方形;
②试探索:将正方形ABCD沿![]() 轴向左平移多少个单位长度时,点C恰好落在双曲线
轴向左平移多少个单位长度时,点C恰好落在双曲线![]() (
(![]() >
>![]() )上.
)上.

参考答案:
【答案】(1)A![]() ,B
,B![]() ;(2)①证明见解析②点C恰好落在双曲线
;(2)①证明见解析②点C恰好落在双曲线![]() (
(![]() >
>![]() )上.
)上.
【解析】试题分析:(1)分别令x=0,求出y的值;令y=0,求出x的值即可得出点B与点A的坐标;
(2)①过点D作DE⊥x轴于点E,由全等三角形的性质可得出△AOB≌△DEA,故可得出AB=AD,再利用待定系数法求出直线AD的解析式即可得出AB⊥AD,由此可得出结论;
②过点C作CF⊥y轴,利用△AOB≌△DEA,同理可得出:△AOB≌△BFC,即可得出C点纵坐标,如果点在图象上,利用纵坐标求出横坐标即可.
解:(1)∵令x=0,则y=2;令y=0,则x=1,
∴A(1,0),B(0,2).
故答案为:(1,0),(0,2);
(2)①过点D作DE⊥x轴于点E,
∵A(1,0),B(0,2),D(3,1),
∴AE=OB=2,OA=DE=1,
在△AOB与△DEA中,
![]() ,
,
∴△AOB≌△DEA(SAS),
∴AB=AD,
设直线AD的解析式为y=kx+b(k≠0),
∴![]() ,
,
解得![]() ,
,
∵(﹣2)×=﹣1,
∴AB⊥AD,
∵四边形ABCD是正方形;
②过点C作CF⊥y轴,
∵△AOB≌△DEA,
∴同理可得出:△AOB≌△BFC,
∴OB=CF=2
∵C点纵坐标为:3,
代入y=,
∴x=1,
∴应该将正方形ABCD沿X轴向左平移2﹣1=1个单位长度时,点C的对应点恰好落在(1)中的双曲线上.
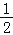
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线a∥b,b∥c,c∥d,则a与d的关系是什么?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】据新安晚报报道,2019年安徽省全年进出口总额为687.3亿美元,其中687.3亿用科学计数法表示为( )
A.6.873×108B.6.873×1010C.6.873×1011D.687.3×108
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句正确的是( )
A.相等的角是对顶角
B.不是对顶角的角都不相等.
C.不相等的角一定不是对顶角
D.有公共点且和为180°的两个角是对顶角. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的有( ) ①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.2·1·c·n·j·y
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,直线a、b相交于O,b∥c,则a与c的位置关系是( )
A.平行
B.相交
C.重合
D.平行或重合 -
科目: 来源: 题型:
查看答案和解析>>【题目】学校操场的环形跑道长400米,小聪的爸爸陪小聪锻炼,小聪跑步每秒行2.5米,爸爸骑自行车每秒行5.5米,两人从同一地点出发,反向而行,每隔_____秒两人相遇一次.
相关试题

